TLS: Jaki rozmiar powinien mieć klucz prywatny?

06 Mar 2020

diffie-hellman  ecc  https  private-key  rsa  security  ssl  tls 

Share on:

Kryptografia klucza publicznego, zwana także kryptografią asymetryczną (ang. Public-Key Cryptography lub Asymmetric Cryptography) zakłada, że każda transmisja danych używa dwóch różnych kluczy, które występują w parach i są ze sobą w pewien sposób połączone — jeden z nich, klucz publiczny, wykorzystywany jest do szyfrowania wiadomości i weryfikacji podpisów, a drugi, klucz prywatny (o którym będziemy rozmawiać), do deszyfrowania wiadomości i generowania podpisów. Co istotne, ten rodzaj kryptografii pozwala udostępnić jeden z tych kluczy (klucz publiczny) każdemu do użytku, natomiast drugi z nich (klucz prywatny) powinien być maksymalnie chroniony.

Przeciwieństwem tego rodzaju szyfrowania jest kryptografia symetryczna, w której obie strony komunikacji uzgadniają jeden, wspólny i tajny klucz wykorzystywany do szyfrowania i deszyfrowania. Widzimy, że ilość stosowanych kluczy jest jedną z głównych różnic między obydwoma rodzajami kryptografii, z której też w pewnym sensie wynikają dalsze różnice, np. rozmiar kluczy czy szybkość działania danego kryptosystemu.

Poniżej znajduje się bardzo przejrzyste i proste porównanie, które przedstawia wykorzystanie kluczy w każdym z rozwiązań:

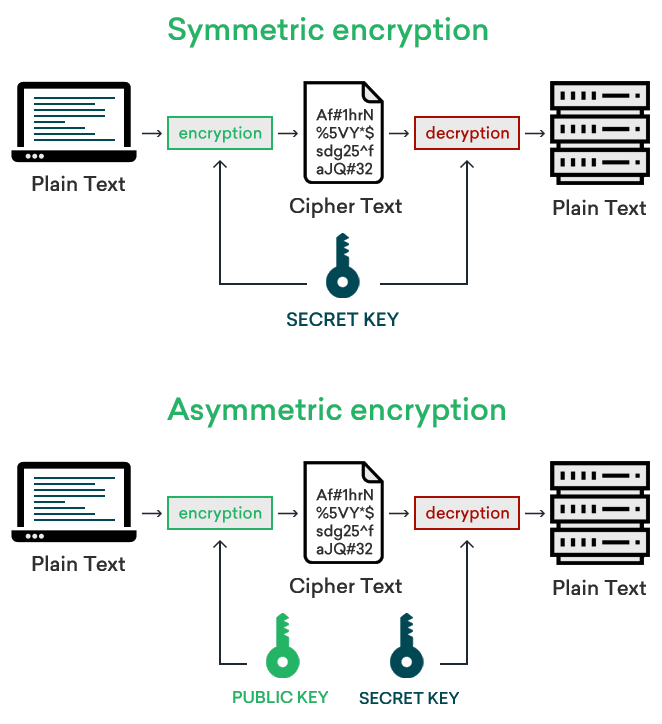
Szyfrowanie oraz deszyfrowanie są tylko jedną z dwóch najważniejszych funkcji kryptografii asymetrycznej (oczywiście także symetrycznej jednak w tym wpisie skupimy się bardziej na tej pierwszej). Drugą jakże istotą są podpisy cyfrowe (ang. Digital signatures), które służą do potwierdzenia tożsamości nadawcy jak i treści przesyłanej wiadomości (jej autentyczności). Stosowanie podpisu cyfrowego gwarantuje, że przesyłka pochodzi od deklarowanego nadawcy, oraz że jej zawartość nie została zmieniona. Klucz publiczny wykorzystywany jest do weryfikacji podpisów, natomiast klucz prywatny służy do ich generowania. Widzisz teraz, że algorytm asymetryczny to tak naprawdę „dwa algorytmy”, jeden, który służy do szyfrowania asymetrycznego, a drugi do podpisów cyfrowych. Chociaż mają te same podstawowe operacje matematyczne i format kluczy, robią różne rzeczy na różne sposoby.

To tyle tytułem wstępu, który jest dobrym punktem wyjściowym do dalszych rozważań. W tym wpisie chciałbym jednak omówić najczęściej stosowane rodzaje kluczy prywatnych zaliczane do jednych z najważniejszych obecnie technik kryptografii asymetrycznej:

Postaram się odpowiedzieć na zadane pytanie w tytule tego wpisu, czyli jaki powinien być rozmiar kluczy prywatnych, dlaczego ma istotne znaczenie dla zapewnienia bezpieczeństwa komunikacji oraz jaki ma wpływ na wydajność, a także, dlaczego nie jest jedynym i najważniejszym parametrem związanym z bezpieczeństwem obu systemów kryptografii asymetrycznej. Omówię także, czym tak naprawdę są klucze prywatne i jaką pełnią funkcję w komunikacji TLS oraz przedstawię kilka dodatkowych kwestii związanych z tym rodzajem kryptografii.

Rozważania zacznę od algorytmu (czyli funkcji matematycznej, która przekształca tekst jawny w tekst zaszyfrowany) RSA, ponieważ na jego przykładzie najlepiej można zaobserwować potencjalny problem rozmiaru klucza, a następnie omówią klucze ECC oparte na krzywych eliptycznych (na ich temat możesz poczytać w artykule Introducing Elliptic Curves), które znacznie omawiany problem niwelują. Mam nadzieję, że po przeczytaniu tego artykułu, zrozumiesz, dlaczego bezpieczeństwo klucza zależy w dużej mierze od jego rozmiaru i zastosowanego algorytmu, oraz dlaczego niektóre algorytmy są łatwiejsze do złamania niż inne i wymagają większych kluczy dla tego samego poziomu bezpieczeństwa.

W celu dokładnego zgłębienia tematu i poszerzenia wiedzy na temat kryptografii oraz protokołów SSL/TLS polecam zapoznać się z poniższą literaturą:

Miej także na oku archiwum Cryptology ePrint Archive, będące zbiorem prac badawczych w dziedzinie kryptologii (czyli połączenia kryptografii i kryptoanalizy). Moim zdaniem jest to świetne źródło wiedzy, które zapewnia dostęp do najnowszych badań i zgłębia wiele zagadnień związanych z bezpieczeństwem.

Czym jest klucz prywatny w infratrukturze PKI? #

Klucz prywatny oraz klucz publiczny są częścią infrastruktury klucza publicznego (ang. PKI - Public Key Infrastructure), która jest powszechnie stosowana w przypadku certyfikatów SSL. PKI jest systemem, który definiuje zbiór zasad i procedur, niezbędnych do świadczenia mechanizmów uwierzytelniania, szyfrowania czy integralności — i to wszystko za sprawą klucza publicznego, prywatnego oraz certyfikatów elektronicznych.

Bardzo dobrą analogią pokazującą zależność obu kluczy i certyfikatu, jest zamknięta skrzynka pocztowa. Miejsce na pocztę jest ujawnione i publicznie dostępne stąd jego lokalizacja (adres) może być traktowana jako klucz publiczny. Co więcej, każda taka skrzynka ma przypisany do niej specjalny znacznik, który zawiera informacje o właścicielu (dzięki czemu jesteś w stanie sprawdzić, czy skrzynka należy właśnie do niego) oraz wyjątkowy skrót/identyfikator (aby upewnić się, że znacznik nie został zmodyfikowany) — a wszystko po to, aby zapewnić ochronę wymiany poufnych informacji. Tym znacznikiem jest certyfikat, który potwierdza, że masz do czynienia z odpowiednim właścicielem skrzynki, a nie np. z kimś, kto się pod niego podszywa. Każdy, kto zna adres skrzynki, może do niej podejść i wrzucić wiadomość. Jednak tylko osoba, która posiada specjalny klucz, może otworzyć skrzynkę i przeczytać wiadomość. Podobną analogię możemy zastosować do algorytmów symetrycznych, z tą różnicą, że nie ma tutaj żadnego certyfikatu, oraz że klucz, który został użyty do otwarcia skrzynki, musi być tym, który był używany do jej zamknięcia — co więcej, taki klucz nigdy nie powinien być dostępny publicznie.

Klucz prywatny jest zakodowanym fragmentem danych (np. zawiera dwie liczby pierwsze p i q, które są podstawowym budulcem kluczy RSA), dzięki czemu może być przechowywany w różnych formatach. Wartości klucza prywatnego są kodowane jako, np. format ASN.1 zakodowany w PEM dla RSA i format ANSI X9.62 zakodowany w PEM dla ECC, które określają sposób ich przechowywania w plikach. Format PEM jest najczęściej wykorzystywanym formatem kluczy prywatnych, kluczy publicznych i certyfikatów, umożliwiający przedstawienie ich w postaci znaków drukowalnych, dzięki czemu można je wysłać np. pocztą lub wydrukować i powiesić na tablicy ogłoszeniowej (w przeciwieństwie np. do formatu DER, który jest formatem binarnym, natomiast PEM jest tak naprawdę formatem DER zakodowanym w base64 z dodanymi nagłówkami). Większość plików w formacie PEM, które zobaczymy, jest generowana przez OpenSSL podczas generowania lub eksportowania klucza prywatnego, publicznego oraz certyfikatów X509. Co istotne, PEM można podzielić na dwa dodatkowe formaty: PKCS #1 i PKCS #8, które obejmują formaty klucza publicznego i prywatnego. Widzisz, że jest to trochę pogmatwane, dlatego więcej informacji na ten temat znajdziesz w artykule ASN.1 key structures in DER and PEM.

Podczas tworzenia klucza prywatnego, jest on najczęściej tworzony wraz z żądaniem podpisania certyfikatu (ang. CSR - Certificate Signing Request), które to przesyłane jest do urzędu certyfikacji w celu utworzenia certyfikatu SSL. Można wyciągnąć z tego prawidłowy wniosek, że z każdym certyfikatem cyfrowym jest skojarzona odpowiednia para kluczy kryptograficznych.

Do czego służy klucz prywatny? #

Na samym początku powiedzieliśmy, że klucz prywatny służy do deszyfrowania danych, które są zaszyfrowane kluczem publicznym. Dobrze, a czy na pewno? I czy jest możliwe wykonanie operacji odwrotnej, tj. zaszyfrowanie kluczem prywatnym i odszyfrowanie kluczem publicznym? W przypadku kryptografii asymetrycznej klucz prywatny i klucz publiczny mają te same właściwości matematyczne, więc w teorii można używać ich zamiennie. Nie mają one jednak tych samych właściwości bezpieczeństwa — klucz publiczny jest zwykle łatwy (łatwiejszy) do odgadnięcia na podstawie klucza prywatnego. Istotne jest także to, że klucz prywatny ma jeszcze kilka dodatkowych właściwości, których nie ma klucz publiczny. Ogólnie rzecz biorąc, klucz publiczny nie jest właściwym typem obiektu matematycznego do użycia w algorytmie deszyfrującym, a klucz prywatny nie jest właściwym typem obiektu matematycznego do użycia w algorytmie szyfrowania. Cały sens asymetrycznego szyfrowania kluczem polega na tym, że klucz, którego używasz do szyfrowania, nie może być użyty do odszyfrowania — potrzebujesz jego odpowiednika, którym jest klucz prywatny.

Nie przeprowadza się procesu szyfrowania za pomocą klucza prywatnego ani nie dokonuje deszyfrowania za pomocą klucza publicznego, ponieważ nie ma to tak naprawdę sensu (matematycznie jest to pewnie możliwe). Podobnie jak nie wykonujesz podpisywania kluczem publicznym — do podpisania potrzebujesz tylko jednego klucza, a jest to klucz prywatny — ponieważ podpisy są weryfikowane za pomocą odpowiedniego klucza publicznego. Niezwykle ważne jest, aby wyłapać tę różnicę, która została przedstawiona w RFC 4346 - Glossary B:

public key cryptography - a class of cryptographic techniques employing two-key ciphers. Messages encrypted with the public key can only be decrypted with the associated private key. Conversely, messages signed with the private key can be verified with the public key.

Z drugiej strony, co w przypadku, kiedy serwer chce wysłać zaszyfrowane dane do klienta? Skoro posiada tylko klucz prywatny, w jaki sposób zaszyfruje wiadomości? Aby odpowiedzieć na te pytania, musimy wiedzieć, że kryptografia oparta na RSA/ECC wykorzystywana jest najczęściej tylko na początkowym etapie uzgadniania za pomocą protokołu TLS (ang. TLS Handshake) i służy głównie do określenia, w jaki sposób będzie przeprowadzane uwierzytelnianie serwera i (w razie potrzeby) uwierzytelnianie klienta — tak naprawdę nie zajmuje się faktycznym szyfrowaniem danych.

Dokładna metoda używana do uwierzytelniania jest określana przez wynegocjowany zestaw szyfrów (ang. Cipher Suite). Jest to w zasadzie zestaw algorytmów potrzebnych do zabezpieczenia połączenia sieciowego za pośrednictwem protokołu SSL/TLS. Klient i serwer kontaktują się ze sobą i wybierają odpowiedni szyfr, który będzie używany podczas dalszej komunikacji i wymiany wiadomości. Co istotne, zestaw szyfrów określa także siłę klucza sesji, który jest uzgodniony między klientem a serwerem podczas nawiązywania połączenia TLS. Definiuje on również metodę używaną do ustanowienia takiego klucza, np. właściwość nowoczesnych mechanizmów uzgadniania kluczy, która zapewnia, że ​​klucza prywatnego certyfikatu nie można użyć do odzyskania kluczy sesji (dzięki temu złamany klucz przedstawiony w certyfikacie nie może zostać użyty do odtworzenia starych kluczy sesji).

Natomiast w celu określenia, w jaki sposób dane będą szyfrowane, najczęściej wykorzystywane są dodatkowe klucze prywatne i publiczne, osobne po stronie serwera i klienta, dla których podstawą (najczęściej) jest algorytm wymiany kluczy Diffie-Hellman (DH). Algorytm DH nie nadaje się do uwierzytelniania, za to nadaje się świetnie do wymiany klucza współdzielonego, którym szyfruje się faktyczne dane. Ponadto Diffie-Hellman jest algorytmem wymiany kluczy w obie strony: odbiorca wysyła swoją połowę („klucz publiczny DH”), nadawca oblicza swoją połowę, uzyskuje klucz, szyfruje, wysyła całą partię do odbiorcy, odbiorca oblicza klucz i na koniec go deszyfruje.

Ponieważ algorytmy RSA/ECC oraz DH nie robią tego samego, możesz preferować jeden nad drugim w zależności od kontekstu użycia. Możesz oczywiście użyć klucza publicznego/prywatnego RSA/ECC jako algorytmu wymiany klucza, jednak nie jest to zalecane (koniecznie zerknij na artykuł Stop using RSA key exchange). Wniosek z tego taki, że DH jest używany do generowania publicznego wspólnego sekretu w celu późniejszego wykorzystania symetrycznego klucza prywatnego do faktycznego szyfrowania danych. Co istotne, jego podstawa matematyczna opiera się albo na liczbach pierwszych, albo na krzywych eliptycznych. Należy także wiedzieć, że w idealnym przypadku Diffie-Hellman powinien być używany w połączeniu z uznaną metodą uwierzytelniania (RSA/ECC), taką jak podpisy cyfrowe, w celu weryfikacji tożsamości.

Dobrze, a w jaki sposób działa algorytm DH? Pozwolę sobie przetłumaczyć bardzo ciekawe wyjaśnienie, którego autorem jest Joshua Davies, autor książki Implementing SSL/TLS Using Cryptography and PKI. Po pierwsze, stosując protokół Diffie-Hellman, nadawca i odbiorca mogą bezpiecznie uzgodnić wspólną liczbę, wykorzystując ją następnie jako klucz w klasycznym protokole kryptograficznym.

Wymiana kluczy Diffiego-Hellmana, choć błyskotliwa, jest w rzeczywistości dość łatwa do zrozumienia. Możesz nawet wyobrazić sobie dwie osoby stosujące ten protokół, wykrzykując do siebie liczby w zatłoczonym pokoju, każda z ołówkiem i papierem do obliczenia tymczasowych wyników. Jeśli ty i ja znaleźliśmy się w takiej sytuacji, ryzykując irytacją innych osób w pokoju, moglibyśmy przeprowadzić bezpieczną wymianę kluczy. Zacząłbyś od wybrania dwóch losowych liczb p i g. Krzyczysz je przez cały pokój do mnie i każdy z nas je zapisuje.

Następnie wybierasz losowo liczbę a i zapisujesz ją. Nie podajesz mi jednak tej liczby — zamiast tego znajdujesz wynik równania ga%p (resztę, gdy ga jest podzielone przez p). Następnie krzyczysz do mnie, podając wynik równania, a ja go zapisuję. Teraz robię to samo z moim własnym sekretnym numerem a i wykrzykuję wynik równania po mojej stronie, który zapisujesz.

Teraz obliczasz Twoje równanie (gb%p)a%p, a ja obliczam moje równanie (gb%p)a%p uzyskując w efekcie ten sam wynik obu obliczeń. W konsekwencji tylko Ty i ja znamy wynik końcowy a żadna z osób w pokoju nie jest w stanie odwrócić tych operacji. Warto wspomnieć, że istnieją pewne ograniczenia dotyczące używanych liczb, np. p musi być liczbą pierwszą, a g musi być jej pierwiastkiem pierwotnym.

Dzięki tym dwóm podstawowym elementom konstrukcyjnym można ustanowić podstawę bezpiecznego kanału komunikacyjnego: najpierw przeglądarka i serwer działają w ramach wymiany kluczy Diffiego-Hellmana, a następnie uzgadniają bezpieczny algorytm kryptograficzny, aby używać go jako faktyczny klucz do szyfrowania i deszyfrowania.

Pamiętajmy jednak, że to nie wszystko, ponieważ nie wystarczy po prostu zaszyfrować wiadomość, gdyż można dokonać jej modyfikacji bez faktycznego jej odszyfrowania, np. usuwając jej część, w wyniku czego ani nadawca, ani odbiorca nie mieliby nigdy możliwości rozpoznania skróconej wiadomości. Tak więc, aby prawidłowo ustanowić bezpieczny kanał komunikacyjny w niezabezpieczonym medium, obie strony muszą najpierw uzgodnić algorytm kryptograficzny, następnie algorytm weryfikacyjny, a następnie przeprowadzić bezpieczną wymianę kluczy, ale zanim to zrobią, muszą najpierw uwierzytelnić się nawzajem.

Widzimy tym samym, że uzgadnianie SSL/TLS składa się z wielu elementów. Najpierw klient ustanawia publiczne, niezabezpieczone połączenie z serwerem. Zanim jednak wyśle ​​jakiekolwiek potencjalnie wrażliwe dane (czyli w ogóle jakiekolwiek dane), wykonuje uzgadnianie SSL/TLS, informując serwer, które algorytmy wymiany kluczy publicznych, szyfrowania, weryfikacji i podpisu cyfrowego rozumie. Z takiego zestawu serwer wybiera ten, który jest przez niego obsługiwany i inicjuje wymianę kluczy przy użyciu wybranego algorytmu (w pierwszej wersji był to Diffie-Hellman lub RSA).

Pierwszym krokiem w obu przypadkach jest jednak zwrócenie podpisanego certyfikatu, który przynajmniej zawiera nazwę hosta serwera dokładnie tak, jak zażądała tego przeglądarka, klucz publiczny odpowiadający RSA lub DSA (w zależności od tego, który cyfrowy algorytm podpisu zastosowano) oraz podpis wygenerowany przez urząd certyfikacji, któremu przeglądarka ufa. Wymiana kluczy jest kontynuowana, gdy serwer podpisuje wymianę kluczy, co potwierdza posiadanie klucza prywatnego odpowiadającego kluczowi publicznemu w certyfikacie. Klient i serwer wymieniają się następnie tymi kluczami, z których jeden wykorzystywany jest do szyfrowania, a drugi do weryfikacji. Po wymianie kluczy każdy kolejny pakiet jest szyfrowany i uwierzytelniany za pomocą dwóch wybranych algorytmów.

Dokładny opis działania algorytmu DH znajdziesz w artykule What is the Diffie–Hellman key exchange and how does it work?.

W przypadku SSL/TLS tak naprawdę nie szyfrujemy rzeczywistych danych za pomocą RSA/ECC/DH a jedynie klucz symetryczny, który to potem jest wykorzystywany przez obie strony komunikacji do szyfrowania faktycznych wiadomości. Natomiast nawet gdyby była możliwość szyfrowania za pomocą klucza prywatnego RSA/ECC nadawcy, każdy mógłby dokonać zdeszyfrowania za pomocą odpowiedniego klucza publicznego, więc szyfrowanie byłoby bezcelowe. Szyfrowanie kluczem prywatnym lub podpisywanie kluczem publicznym jest technicznie możliwe, np. za pomocą RSA, jednak nie ma to żadnej właściwości bezpieczeństwa.

Niezwykle istotne jest także to, że w komunikacji SSL/TLS, podczas uzgadniania, serwer uwierzytelnia się (potwierdza swoją tożsamość) klientowi za pomocą mechanizmu certyfikatu. Wspominam o tym, gdyż ta właściwość umożliwia przeprowadzanie uwierzytelniania poprzez szyfrowanie, ponieważ jeśli wiadomość zaszyfrowano kluczem publicznym danego podmiotu, to znaczy, iż można odszyfrować ją jego kluczem prywatnym, co dowodzi z kolei, że taki klucz (po stronie serwera) jest prawidłowy, tj. przypisany do serwera i przeznaczony tylko dla niego. Klient dodatkowo weryfikuje certyfikat SSL serwera za pomocą urzędu certyfikacji, który go wystawił. Potwierdza to, że serwer jest tym, za kogo się podaje i że klient wchodzi w interakcje z faktycznym właścicielem domeny.

Niezależnie jednak od zastosowanego typu kryptografii asymetrycznej, pamiętajmy, że klucz prywatny jest kluczem tajnym (co do zasady powinien być traktowany jako tajny, ponieważ jeśli zostanie w jakikolwiek sposób udostępniony, to nie jest już ani tajny, ani prywatny), który służy do deszyfrowania i podpisywania, natomiast klucz publiczny może być udostępniony każdemu, i służy do szyfrowania i weryfikacji podpisów.

Połączenie kryptografii symetrycznej i asymetrycznej #

W przypadku kryptografii wykorzystującej algorytm RSA, czyli obecnie występującej najczęściej, klucz publiczny tworzony jest na podstawie klucza prywatnego oraz wyjątkowo trudnego do złamania iloczynu losowo wybranych liczb pierwszych. Jego użycie pozwala uniknąć słabości szyfrowania symetrycznego, w którym klucz tajny jest współdzielony przez obie strony komunikacji (tzw. problem dystrybucji klucza polegający na tym, że tajny klucz należy przesłać do systemu odbierającego przed wysłaniem właściwej wiadomości, wykluczając ujawnienie go osobom trzecim). Istnieje drugi rodzaj kryptografii asymetrycznej oparty na krzywych eliptycznych, którego podstawą jest trudność w rozwiązaniu problemu logarytmu dyskretnego. Dzięki temu klucze wykorzystujące krzywe stają się bezpieczniejsze bez zwiększenia ich rozmiaru. Temat zostanie poruszony szerzej w jednym z następnych rozdziałów.

Pozwolę sobie w tym momencie przytoczyć genialną analogię (pochodzi ona z artykułu Explaining public-key cryptography to non-geeks), która zobrazuje zależność, jaka istnieje między kluczem prywatnym a publicznym oraz przedstawi różnicę między szyfrowaniem symetrycznym i asymetrycznym (niech będzie to uzupełnienie przykładu ze skrzynką pocztową).

Wyobraź sobie sejf z zamkiem, który jest używany tylko przez dwie osoby (zgodnie z tradycją są to Bob i Alice) do wkładania, przechowywania i wyciągania bardzo poufnych dokumentów. Typowy zamek ma tylko dwa stany: zamknięty i otwarty. Każdy, kto ma kopię klucza, może odblokować sejf, jeśli jest zablokowany, i odwrotnie. Kiedy Bob zamyka sejf i wysyła taką informację do Alice, wie, że może ona użyć swojej kopii klucza, aby odblokować zamek w sejfie. W zasadzie tak działa to, co nazywa się kryptografią symetryczną: jeden tajny klucz jest używany zarówno do szyfrowania, jak i deszyfrowania, a obie strony komunikacji używają tego samego klucza.

A teraz wyobraź sobie, że Bob posiada sejf ze specjalnym zamkiem, którego blokada polega na zastosowaniu trzech stanów zamiast dwóch:

Można to przedstawić na poniższej grafice:

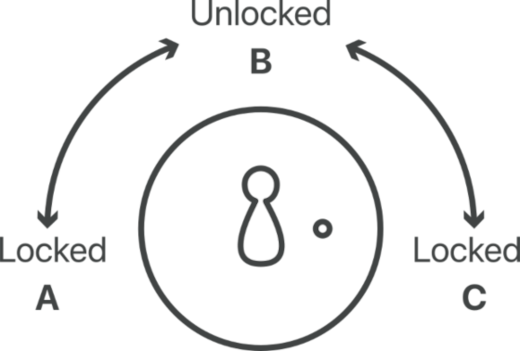
Główną różnicą jest to, że zamiast jednego klucza do takiego zamka pasują dwa klucze:

Oznacza to, że jeśli sejf jest zamknięty i kluczyk jest obrócony do pozycji A, tylko klucz nr 2 może go odblokować, obracając zamek w prawo do pozycji B (odblokowany). Jeśli sejf jest zablokowany w pozycji C, tylko klucz nr 1 może go odblokować, obracając zamek w lewo, do pozycji B. Innymi słowy, każdy klucz może zablokować (zaszyfrować) sejf — ale po zablokowaniu tylko drugi klucz może go odblokować (odszyfrować). Bob może utworzyć specjalny klucz, który będzie miał magiczne właściwości i który będzie tylko dla niego, oraz drugi specjalny klucz, na podstawie tego pierwszego, który udostępni swoim znajomym. Dzięki temu każdy, kto posiada udostępniony klucz przez Boba, może wysłać mu poufne dane i mieć pewność, że tylko on będzie w stanie je odczytać. Dzieje się tak, ponieważ jeśli znajomy Boba zamknie sejf kluczem publicznym, który obraca się od lewej do prawej, to tylko klucz, który może obracać się od prawej do lewej (czyli klucz prywatny), może go odblokować.

Przy okazji, każdy ze znajomych Boba ma pewność, że sejf faktycznie pochodzi od niego, a nie od kogoś, kto się podszywa pod Boba. Poufną informację można zaszyfrować tylko za pomocą klucza publicznego i odszyfrować tylko za pomocą klucza prywatnego — czyli każdy może zaszyfrować dane kluczem publicznym, ale tylko właściciel klucza prywatnego może je odszyfrować, dzięki czemu każdy, kto ma klucz publiczny może bezpiecznie przesłać dane do właściciela klucza prywatnego. Ponadto każdy może sprawdzić, czy dane, które otrzyma od właściciela klucza prywatnego, faktycznie pochodzą z tego źródła, a nie od osoby, która podszywa się pod niego.

Teraz widzimy, że problem, który rozwiązuje kryptografia klucza publicznego, polega na tym, że nie ma wspólnego sekretu (klucza). Przy szyfrowaniu symetrycznym musimy w sposób domniemany ufać wszystkim zaangażowanym w komunikacji stronom, że utrzymają klucz w tajemnicy. Jest to niewątpliwie główna kwestia, o której należy pamiętać przy wyborze konkretnego rozwiązania i powinna być ona znacznie większym problemem niż wydajność (którą można złagodzić dzięki połączeniu kryptografii symetrycznej i asymetrycznej).

Spójrzmy na przykładzie komunikacji klienta z serwerem HTTP (tym razem z szerszym wyjaśnieniem):

Podgląd pochodzi z artykułu The SSL/TLS Handshake: an Overview

Pokazuje on doskonale, że klucz prywatny oraz publiczny wykorzystywane są na jednym z początkowych etapów komunikacji. Serwer, w komunikacie ServerHello wysyła do klienta parametry połączenia TLS oraz certyfikat wraz z kluczem publicznym. Serwer przedstawiając się klientowi, przekazuje mu swój certyfikat, jako dowód tożsamości. Tym samym serwer mówi: „oto mój certyfikat, dzięki któremu będziesz mógł sprawdzić, że jestem tym, za kogo się podaję” (a nie kimś, kto ma złe zamiary). Aby zapewnić autentyczność klucza publicznego zawartego w certyfikacie, musi on być podpisany przez specjalną instytucję, czyli urząd certyfikacji (ang. CA - Certificate Authority). Wydanie certyfikatu ma miejsce wtedy i tylko wtedy, gdy rejestrujący może udowodnić, że jest właścicielem domeny, dla której został wydany certyfikat. Jeżeli proces weryfikacji przebiegł poprawnie, po wydaniu certyfikatu umieszczamy klucz prywatny oraz łańcuch certyfikatów po stronie serwera.

Po zweryfikowaniu certyfikatu następuje tzw. wymiana klucza (ang. Key Exchange). Jest to taki proces w komunikacji TLS, dzięki któremu istnieje możliwość ustanowienia wspólnego sekretu między dwiema stronami komunikacji. Klient i serwer wymieniają losowe liczby i specjalny ciąg nazywany tajnym kluczem wstępnym (ang. Pre-Master Secret). Podczas tego procesu, klient szyfruje go kluczem publicznym, zaś serwer podpisuje (szyfruje) go kluczem prywatnym. Taki klucz wstępny jest łączony z dodatkowymi danymi umożliwiającymi klientowi i serwerowi utworzenie wspólnego sekretu (ang. Master Secret). Ten wspólny sekret jest używany przez klienta i serwer do generowania kluczy sesji, które są wykorzystywane do haszowania oraz do faktycznego szyfrowania danych. Widzimy, że w kryptosystemach mieszanych kryptografia klucza publicznego jest wykorzystywana do ustalenia wspólnego sekretu między obiema stronami, a wspólny sekret służy do tworzenia kluczy symetrycznych, które mogą być używane do szyfrowania wymienianych danych.

Na tym etapie wykorzystuje się najczęściej dwa algorytmy (tak naprawdę zalecanym jest ten drugi):

W każdym z tych dwóch przypadków RSA wykorzystywany jest do uwierzytelniania, a DHE jak i ECDH/ECDHE służą do wyprowadzenia wspólnego i tajnego klucza między klientem a serwerem, który jest później używany do szyfrowania (symetrycznego) komunikacji po zakończeniu uzgadniania (czyli do szyfrowania faktycznych danych). Istnieje jeszcze jedna technika wymiany kluczy, gdzie klucz prywatny serwera wykorzystuje algorytm RSA, który służy jednocześnie do uwierzytelniania oraz do wymiany kluczy (czyli jest wykorzystywany do jednego i drugiego).

Wiemy już, że można wykorzystać obie techniki, tj. RSA do podpisywania i DH do uzgadniania (np. zestawy szyfrów TLS_*DH*_RSA_WITH_*) lub RSA do obu tych czynności (tj. TLS_RSA_WITH_*). Obecnie jednak najczęściej stosowaną metodą jest wykorzystanie DH do wymiany kluczy, które uwierzytelnione są za pomocą RSA lub ECDSA (ang. Elliptic Curve Digital Signature Algorithm), np. TLS_ECDHE_RSA_WITH_* lub TLS_ECDHE_ECDSA_WITH_*. Na dzień dzisiejszy, pomimo wielu opcji dostępnych w TLS, prawie wszystkie certyfikaty są oparte na protokole RSA. Widzisz teraz, że typ klucza narzuca w pewien sposób z góry rodzaj wykorzystywanego szyfru oraz metodę weryfikacji. O szyfrach jednak porozmawiamy później.

Dlaczego w takim razie wykorzystuje się DH, skoro praktycznie to samo można zrobić za pomocą RSA? Protokół DH zapewnia szybką procedurę uzgadniania klucza z możliwością jego szybkiego usuwania, natomiast generowanie kluczy RSA jest niezwykle kosztowne i pozbawione możliwości posprzątania po sobie. Dzięki stosowaniu wymiany kluczy DH zaraz po zakończeniu sesji wszystkie kopie kluczy prywatnych DH, wyprowadzony klucz wstępny czy wyprowadzony klucz główny mogą zostać usunięte. DH jest używany razem z RSA, aby uzyskać kanał komunikacyjny, który jest zarówno uwierzytelniony, jak i bezpieczny.

Jak już wspomniałem, faktycznym szyfrowaniem i deszyfrowaniem wiadomości w jednej sesji komunikacyjnej zajmuje się symetryczny klucz sesji wynegocjowany (a nie szyfrowany i wysyłany) na późniejszym etapie zestawiania połączenia. Dlaczego? Chodzi o zwiększenie szybkości działania dość wolnego algorytmu szyfrowania kluczem publicznym — algorytm szyfrowania symetrycznego jest mniej złożony, przez co działa szybciej. Mówiąc najprościej, cały proces może wyglądać następująco: oryginalna wiadomość jest szyfrowana szyfrem symetrycznym, przy użyciu tworzonego klucza (albo stałego, albo tymczasowego). Klucz ten jest szyfrowany z kolei kluczem publicznym adresata i dołączany do zaszyfrowanej wiadomości. Odbiorca używa swojego klucza prywatnego do odzyskania klucza tymczasowego, który z kolei służy do szybkiego rozszyfrowania wiadomości. Więcej informacji na ten temat uzyskasz w świetnym artykule The First Few Milliseconds of an HTTPS Connection.

Kryptografia z kluczem symetrycznym jest generalnie szybsza i trudniejsza do złamania, natomiast kryptografia asymetryczna jest wolniejsza, ale lepsza do rozpowszechniania (publikowania). Dwa najbardziej popularne algorytmy asymetryczne to RSA i ECC. Istnieje też wiele symetrycznych algorytmów szyfrowania jednak istotne jest aby zrozumieć, że mogą one działać tylko na dwa sposoby: jako szyfry strumieniowe, które szyfrują wiadomości bit po bicie (litera po literze, liczba po liczbie) oraz szyfry blokowe, które szyfrują wiadomości w blokach danych. Najpopularniejszym obecnie szyfrem strumieniowym jest ChaCha20. Jednak to szyfry blokowe są bardziej powszechne. Najczęściej stosowane algorytmy szyfrowania symetrycznego (blokowe) obejmują AES-128, AES-192 i AES-256.

Odpowiedź na to, dlaczego takie mieszane rozwiązanie jest optymalne, wynika z różnic między szyfrowaniem symetrycznym i asymetrycznym:

Szyfrowanie asymetryczne jest bardziej wymagające, ponieważ polega na realizacji szyfrowania i możliwości opublikowania sposobów tego procesu (klucz publiczny) bez ujawniania sposobów procesu odwrotnego, jakim jest deszyfrowanie (klucz prywatny). Praktyczna implementacja wymaga trochę matematyki, podczas gdy szyfrowanie symetryczne polega głównie na mieszaniu (ang. mixed), tj. używa tajnego klucza, którym może być liczba, słowo lub ciąg losowych znaków, który to mieszany jest ze zwykłym tekstem wiadomości, aby zmienić jej treść w określony sposób. W przypadku kluczy symetrycznych bezpieczeństwo, które zapewniają, rośnie wykładniczo wraz z ich długością — dodanie jeszcze jednego bitu podwaja ich odporność na ataki siłowe. W typowych algorytmach szyfrowania symetrycznego klucz jest dosłownie po prostu losową liczbą, której siła opiera się na jej odporności na ataki siłowe, w przypadku których atakujący musiałby wykonać atak z odpowiednią złożonością, aby poprawnie odgadnąć klucz.

Co więcej, istnieje jeszcze jedna ogromna różnica między oboma typami kryptografii w kontekście bezpieczeństwa: za każdym razem, gdy w kluczu znajduje się jakiś wzór, oznacza to słabość w systemie kryptograficznym. To tak samo jak z nami, gdzie w idealnym świecie tworzylibyśmy i zapamiętywali całkowicie przypadkowe hasła. Z racji tego, że jest to dla nas za trudne, tego nie robimy. W naszych hasłach (lub procedurach ich tworzenia) są pewne wzory, które pomagają nam je wygenerować i zapamiętać, i które można odgadnąć lub złamać bez konieczności wypróbowywania każdego możliwego hasła. Klucze RSA mają charakterystyczny wzór: są iloczynem dwóch liczb pierwszych i to właśnie zapewnia pewną słabość. W przypadku klucza symetrycznego nie ma takich wzorców — te klucze są po prostu dużymi, losowo wybranymi liczbami. Ich jakość jest typowo zależna od odpowiedniego źródła (generatora), które wygeneruje takie losowe liczby (czyli zapewni odpowiednią/wystarczającą entropię).

Za nim jednak przejdziemy do podsumowania tego rozdziału, zatrzymajmy się na chwilę. Dawno temu, natknąłem się na zestaw kilkunastu pytań, które były prawdopodobnie wykorzystane podczas rozmowy kwalifikacyjnej na stanowisko administratora. Jednym z pytań było: który rodzaj kryptografii jest lepszy, asymetryczny czy symetryczny? Potrafimy już mniej lub bardziej odpowiedzieć, czym są oba rodzaje kryptografii, jednak co to znaczy, że algorytm jest asymetryczny lub symetryczny? Algorytmy kryptografii klucza publicznego, takie jak RSA, są często nazywane algorytmami asymetrycznymi, ponieważ klucz szyfrowania nie jest równy (symetryczny, zgodny) z kluczem deszyfrującym. Ten rodzaj kryptografii narusza pewną harmonię, którą zawiera w sobie kryptografia symetryczna. W następnych rozdziałach będzie trochę matematyki i tam dokładnie zobaczysz tę asymetrię. Natomiast w przypadku algorytmu symetrycznego, nie ma różnic (asymetrii), ponieważ klucz jest jeden — jest w nim zachowana równowaga i zgodność.

Podsumowując: większe rozmiary kluczy kryptograficznych, dwa klucze kryptograficzne zamiast jednego oraz wprowadzenie urzędu certyfikacji — dodatkowe wyszukiwania DNS i czasy odpowiedzi serwera — to z powodu tych dodatkowych obciążeń większość implementacji korzysta z algorytmu hybrydowego. Korzystając z takiego systemu, do szyfrowania nie używa się bezpośrednio konkretnego algorytmu (np. ECC). Klucze publiczne i prywatne są używane jedynie do potwierdzenia tożsamości partnera komunikacji oraz do przesłania czegoś, co da w wyniku symetryczny klucz sesji (klucz tymczasowy używany tylko raz), który to z kolei wykorzystywany jest do wydajnego szyfrowania i deszyfrowania rzeczywistych danych w celu uzyskania najlepszych zalet z obu światów. Nawiązując jeszcze do poprzedniego rozdziału, dzięki takiemu połączeniu komunikacja jest szyfrowana w obie strony, a nie tylko w jedną.

Kryptografia asymetryczna #

Pomówmy teraz trochę o algorytmach, które są tematem tego wpisu, tj. RSA i ECC. Oba typy kluczy mają tę samą ważną właściwość, mianowicie są algorytmami asymetrycznymi (wiemy już, że jeden klucz służy do szyfrowania a drugi do deszyfrowania). Ponadto oba typy kryptografii mają jeszcze jedną wspólną cechę, z której wynika fundamentalna różnica — u podstaw ich bezpieczeństwa leżą dwa następujące problemy matematyczne:

Widzimy, że podstawową kwestią bezpieczeństwa jest odpowiednia trudność (złożoność) w rozwiązaniu podstawowego problemu matematycznego dla danego systemu, która jest tak naprawdę niezbędna dla bezpieczeństwa wszystkich protokołów w rodzinie kluczy publicznych — i tak, u jej podstaw leży problem z faktoryzacją liczb całkowitych w systemach RSA, problem z logarytmem dyskretnym (np. dla Diffie-Hellman) oraz problem logarytmu dyskretnego krzywej eliptycznej dla systemów opartych na krzywych. Postrzegana trudność tych problemów ma bezpośredni wpływ na wydajność, ponieważ dyktuje rozmiary kluczy oraz inne ważne parametry. To z kolei wpływa na wydajność podstawowych operacji arytmetycznych.

Algorytm RSA #

Zacznijmy od pierwszego punktu. Jak wspomniałem na samym wstępie, jednym z najpopularniejszych algorytmów asymetrycznych jest RSA. Niestety, ze względu na złożone operacje matematyczne związane z szyfrowaniem i deszyfrowaniem, algorytmy asymetryczne okazują się dosyć powolne (zwłaszcza sam proces deszyfrowania) w przypadku zetknięcia z dużymi zestawami danych.

Dlaczego? Dochodzimy do pierwszego problemu matematycznego. Dzieje się tak, ponieważ bezpieczeństwo szyfrowania w przypadku RSA opiera się na trudności faktoryzacji (złożoności obliczeniowej) dwóch dużych, losowo wybranych liczb pierwszych (tak naprawdę niezależnie od wykorzystywanego algorytmu, stanowią one nieodłączny element kryptografii asymetrycznej). Odgadnięcie tych liczb nie jest zbyt proste w związku z obliczeniową trudnością rozkładu dużej liczby złożonej na czynniki pierwsze, dlatego rozmiar takiej liczby jest jedną z kluczowych cech skutecznej obrony przed złamaniem kluczy RSA. Czyli, łatwo jest odnaleźć dużą liczbę pierwszą (wykonać mnożenie), ale trudno rozłożyć na czynniki iloczyn dwóch dużych liczb pierwszych (faktoryzacja). Dlatego, aby złamać szyfr RSA, należy rozbić klucz publiczny na dwie liczby pierwsze będące jego dzielnikami.

Znajomość tych liczb pozwala rozszyfrować każdą informację zakodowaną kluczem prywatnym i publicznym. Jednakże nie ma prostej metody rozbijania dużych liczb na czynniki pierwsze. Nie istnieje żaden wzór, do którego podstawiamy daną liczbę i w wyniku otrzymujemy wartości jej czynników. Należy je znaleźć, testując podzielność kolejnych liczb.

Bezpieczeństwo RSA zależy od trudności w rozkładaniu dużych liczb całkowitych na czynniki.

Spójrz na to wyjaśnienie. Wiemy, że klucz publiczny jak i prywatny składają się z dwóch bardzo dużych liczb całkowitych, jednak dla klucza publicznego będą to e i n, zaś dla klucza prywatnego będą to d i n. Widzimy, że te trzy liczby są powiązane w specjalny sposób, zaś n jest częścią wspólną. Kluczową kwestią jest to, że n jest gwarantowana jako iloczyn dwóch liczb pierwszych p i q, tj. n = pq. Jeżeli uda nam się znaleźć e i n oraz dokonać rozkładu n na pq, bardzo łatwo będzie wyliczyć d. Tak więc bezpieczeństwo RSA wymaga, aby faktoryzacja dużej liczby całkowitej była trudna i jest to klucz do zapewnienia bezpieczeństwa tego systemu.

Wiąże się to jednak z większym narzutem, tj. powolnym generowaniem kluczy, zwiększonym zużyciem zasobów przez większy rozmiar takich kluczy czy powolnym deszyfrowaniem. Protokół SSL/TLS wykorzystuje RSA tylko do weryfikacji i ew. wymiany kluczy. Zamiast tego generowany jest klucz symetryczny i przesyłany z powrotem do serwera za pomocą szyfrowania RSA (lub wymiany kluczy DH), a następnie reszta danych jest wymieniana za pośrednictwem takiego klucza wspólnego. Takie podejście jest bardzo racjonalne, ponieważ RSA polega na wykonywaniu obliczeń na bardzo dużych liczbach — w szczególności proces deszyfrowania to przeliczanie dużej liczby do ogromnej potęgi — i nie nadaje się do szyfrowania zbiorczego.

Algorytm RSA opiera się na czymś, co jest naprawdę trudne do rozgryzienia (jednak w teorii możliwe). Jest on mniej bezpieczny niż algorytm symetryczny oparty na wspólnym sekrecie, którego nie da się rozwiązać matematycznie, i który nie opiera się na złożoności problemu matematycznego. Z tego powodu protokół SSL/TLS wykorzystuje RSA tylko do weryfikacji i wymiany kluczy. Dla pozostałej części generowany jest klucz symetryczny (np. 256-bitowy) i przesyłany za pomocą szyfrowania RSA — jeśli jest zaszyfrowany za pomocą klucza publicznego serwera, to tylko serwer (który zna klucz prywatny) może go odszyfrować, co oznacza, że żaden pośrednik w poprzednim kroku nie może znać nowego klucza wspólnego — a następnie reszta danych jest wymieniana za pośrednictwem takiego klucza współdzielonego i algorytmu symetrycznego.

Szyfrowanie symetryczne nie może wykonać początkowych publicznych/prywatnych operacji, które są potrzebna do rozpoczęcia kolejnych procesów odpowiedzialnych za szyfrowanie i deszyfrowanie. Klasyczne kryptosystemy, np. oparte na kryptografii symetrycznej, działają głównie poprzez powtarzanie bardzo prostych operacji bitowych (które dodatkowo można wykonywać równolegle) stąd są znacznie szybsze. Oczywiście kluczowe jest jeszcze posiadanie silnego kryptograficznie generatora liczb losowych, aby zapewnić odpowiednią losowość i bezpieczeństwo (np. ochrona przed zduplikowanymi „losowymi” sekwencjami), a także zapewnienie poprawnej implementacji danego rozwiązania.

Algorytm ECC #

Alternatywą dla RSA jest kryptografia wykorzystująca krzywe eliptyczne, która prezentuje inne matematyczne podejście do szyfrowania, opierające się na arytmetyce obejmującej punkty krzywej. Ponadto wymaga znacznie mniejszych kluczy przy zapewnieniu tego samego (podobnego) poziomu bezpieczeństwa. Siła tego rodzaju kryptografii polega na trudności (złożoności) obliczeniowej logarytmów dyskretnych na krzywych eliptycznych i opiera się na tzw. problemie logarytmu dyskretnego krzywej eliptycznej (ang. ECDLP - Elliptic Curve Discrete Logarithm Problem) i zależy od czasu, jaki jest potrzebny, aby odwrócić funkcję jednokierunkową.

Znalezienie logarytmu dyskretnego jest zaskakująco trudnym zadaniem, i o ile potęgowanie jest szybkie (funkcja jednokierunkowa), to już odwrócenie tej czynności, np. znalezienie dla liczby 177147 potęgi, do której trzeba podnieść 3, jest znacznie trudniejsze (w tym przypadku wystarczy kalkulator). Jeszcze trudniejsze jest jednak rozwiązanie równania g^y = x mod p, gdzie g, y, p i x są pewnymi liczbami pierwszymi, a y jest nieznane. Kryptografia, jaką znamy dzisiaj, polega na trudności w rozwiązaniu tego równania (co jest prawie niemożliwe), ponieważ wykładników musielibyśmy szukać metodą prób i błędów, i nie ma tak naprawdę na to efektywnego rozwiązania zwłaszcza przy odpowiednio dużych, kilkuset cyfrowych liczbach/modułach — nawet gdyby atakujący miał dostęp do całej mocy obliczeniowej na świecie, zbadanie wszystkich możliwości zajęłoby tysiące lat. Problem logarytmu dyskretnego jest podstawowym budulcem tego rodzaju kryptografii (drugi z wymienionych problemów matematycznych).

Odpowiadając na pytanie, czym jest krzywa eliptyczna (zadano mi je dwa razy, jako administrator nie potrafiłem na to pytanie odpowiedzieć jasno, i myślę, że obecnie mimo lepszego zrozumienia tematu, nadal jest to w pewien sposób dla mnie wyzwanie), mówiąc w miarę dokładnie i prosto, jest ona po prostu funkcją algebraiczną reprezentującą zbiór punktów, która podczas kreślenia wygląda jak symetryczna krzywa równoległa do osi x (czyli jest to zbiór punktów na płaszczyźnie, który spełnia określone równanie algebraiczne). Punkty na takiej krzywej nie są tylko zwykłym zbiorem punktów, ponieważ mają strukturę wystarczającą do utworzenia grupy — mówiąc w dużym uogólnieniu, takiego zbioru, który składa się z elementów, np. liczb, oraz dodatkowo pewnego działania gdzie te oba składniki są ze sobą silnie powiązane. Jednak to, co wyróżnia grupy, polega na tym, że jeśli wykonasz pewne operacje, zawsze otrzymasz elementy wewnątrz tej grupy.

Krzywe eliptyczne są obiektami matematycznymi, które pozwalają w łatwy sposób na określenie (wygenerowanie) skończonej i zazwyczaj dużej liczby punktów tej krzywej a wszelkie operacje, które są wykonywane na krzywych, de facto są operacjami arytmetycznymi na ich współrzędnych.

Wiemy już, czym jest krzywa, wiemy, że ma jakieś punkty (współrzędne), jednak czy może zostać w jakiś sposób przedstawiona, aby lepiej ją sobie wyobrazić? Tak, oto przykład krzywej o równaniu y2 = x3 - 3x + 3:

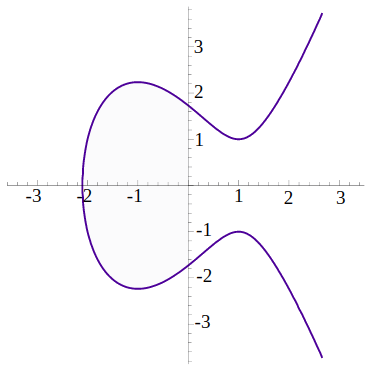
Krzywe eliptyczne wywodzą się od protokołu Diffiego Hellmana (polecam kolejny świetny artykuł na ten temat: Diffie-Hellman: The Genius Algorithm Behind Secure Network Communication, który w miarę prosto wyjaśnia jego działanie), który był jednym z pierwszych praktycznych przykładów wymiany kluczy publicznych. Protokół ten nazywany jest protokołem uzgadniania kluczy i umożliwia dwóm hostom tworzenie i udostępnianie tajnego klucza sesji. Protokół DH i oparty na nim algorytm podpisu cyfrowego (DSA) są obecnie powszechnie używanymi asymetrycznymi systemami kryptograficznymi, które jako podstawę wykorzystują problem logarytmu dyskretnego (ang. DLP - Discrete Logarithm Problem) polegający na znalezienia logarytmu liczby w systemie arytmetycznym z polami skończonymi (czyli takimi, które zawierają skończoną liczbę elementów). Ponieważ potęgowanie w takim polu jest stosunkowo czymś prostym, to jego odwrotność, tj. obliczanie logarytmu, jest już operacją niezwykle trudną.

Wykorzystując swoje właściwości na takim polu skończonym, krzywe eliptyczne działają w sposób inny niż tradycyjny system klucza publicznego (mimo tego, że krzywe są metodą kryptografii opartą także na kluczu publicznym), w którym podstawa jest zbudowana na dużych liczbach pierwszych i faktoryzacji (czyli rozkładu liczby na czynniki). Oczywiście krzywe eliptyczne opierają się także na dużych liczbach pierwszych, ale mogą też wykorzystywać liczby rzeczywiste. Operacje na liczbach rzeczywistych są jednak powolne i niedokładne z powodu zaokrągleń. Co więcej, aby operacje na krzywej eliptycznej były dokładne i wydajniejsze, kryptografia krzywych eliptycznych jest definiowana na polach skończonych, zwanych także polami Galois, na cześć twórcy teorii pola skończonego, Évariste Galois. Te pola nie tylko są wykorzystywana w przypadku krzywych, na pewno spotkałeś się z trybem działania szyfru blokowego GCM, który wykorzystuje hashowanie binarne pola Galois, zapewniając uwierzytelnione szyfrowanie. Więcej na temat tego szyfru możesz poczytać w pracy The Galois/Counter Mode of Operation (GCM) [PDF].

Podobnie jak w przypadku innych form kryptografii klucza publicznego, ECC opiera się na właściwości jednokierunkowej, w której łatwo jest wykonać obliczenia, np. pomnożyć dwie liczby, ale niemożliwe (bądź niezwykle trudne) jest odwrócenie wyników tych obliczeń (rozłożyć liczby na czynniki) w celu odzyskania oryginalnych liczb. ECC wykorzystuje inne operacje matematyczne niż RSA do osiągnięcia tej właściwości.

Bezpieczeństwo ECC zależy od stopnia trudności problemu logarytmu dyskretnego krzywej eliptycznej. Z powodu złożoności arytmetyki jaką wykorzystuje się dla krzywych eliptycznych, oferują one większe bezpieczeństwo, ponieważ ich złamanie wymaga większej ilości obliczeń w porównaniu z np. RSA.

Każda krzywa ma specjalnie wyznaczony punkt nazywany punktem bazowym, który dobrany jest tak, że duża część punktów tej krzywej jest jego wielokrotnością. Aby wygenerować parę kluczy, wybiera się losową liczbę całkowitą, która służy jako klucz prywatny i oblicza się iloczyn punku bazowego z tą losową liczbą, który służy jako odpowiedni klucz publiczny.

Nie wchodząc w detale (głównie ze względu na brak odpowiednich kompetencji; przy okazji bardzo zachęcam do przeczytania tego bardzo prostego i krótkiego wprowadzenia) postaram się to w miarę jasno wyjaśnić. Problem ten polega na znalezieniu odpowiedniej liczby całkowitej R, mając dane punkty P i Q, które zostały umieszczone na krzywej. Mając te trzy punkty np. na płaszczyźnie, łatwo zaobserwować, że prosta przejdzie tylko przez nie (P, Q i R), a znając dwa punkty (P i Q), drugi (R) można łatwo obliczyć. Natomiast mając tylko R, nie można wyprowadzić pozostałych dwóch.

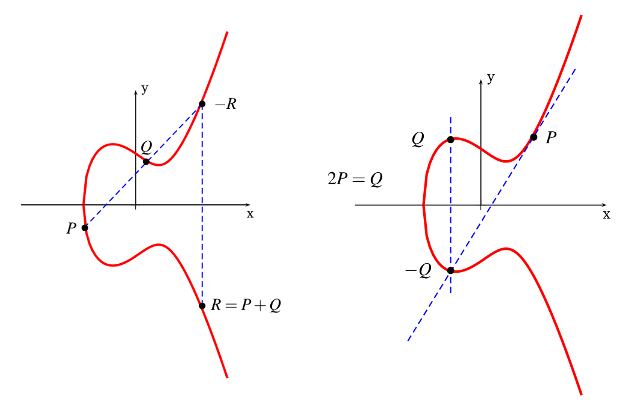
Kluczowe jest to, że pomnożenie punktu jest łatwym zadaniem — to po prostu dodanie punktów do siebie. W ogólnym przypadku problem ten jest obliczeniowo trudny (wymagający dużej złożoności obliczeniowej), ponieważ nie ma algorytmu obliczającego, ile razy P zostało dodane do siebie lub przez jaką liczbę zostało pomnożone, aby dojść do określonego punktu. Jednak istnieją takie typy krzywych, dla których jest on w miarę łatwy (łatwiejszy). Wynika z tego fakt, że istnieją takie krzywe eliptyczne, dla których bardzo łatwo jest znaleźć odpowiednie R i cały szkopuł polega na tym, aby znaleźć taki jej rodzaj, dla którego równianie R = PQ będzie bardzo trudno rozwiązać. Czyli mówiąc najprościej, udzielić odpowiedź na pytanie „ile razy musimy pomnożyć punkt P, aby otrzymać dany punkt R”, co jest niezwykle kosztowne obliczeniowo, a tym samym zwiększa trudność skompromitowania takiej krzywej i uznania jej za nieoptymalną.

Od tego właśnie zależy bezpieczeństwo tego systemu kryptograficznego. Nie ma obecnie znanego rozwiązania tego problemu przedstawionego przez równanie, które tworzy krzywą eliptyczną na wykresie, więc jedynym rozwiązaniem jest sukcesywne sprawdzanie wszystkich możliwych kombinacji w poszukiwaniu jego rozwiązania, czyli wypróbowanie losowych liczb za pomocą techniki siłowej (ang. brute force).

Zdecydowanie wolę proste wytłumaczenia dlatego posłużę się jeszcze opisem zaczerpniętym i przetłumaczonym ze świetnego artykułu Understanding How ECDSA Protects Your Data. Rozmawiając o krzywych eliptycznych w celu ich zrozumienia, można przyjąć bardzo prostą zasadę. Masz równanie matematyczne, które rysuje krzywą na wykresie, następnie wybierasz losowy punkt na tej krzywej i stwierdzasz, że jest to twój punkt wyjścia. Następnie generujesz liczbę losową, która będzie kluczem prywatnym. Następnie, wykonujesz jakieś magiczne równanie matematyczne, używając tej liczby losowej i punktu początkowego — w ten oto sposób otrzymujesz drugi punkt na krzywej, który jest kluczem publicznym.

Kiedy chcesz podpisać jakieś dane (np. plik), użyjesz klucza prywatnego (losowej liczby) z hashem pliku (unikalną liczbą reprezentującą plik) w kolejnym magicznym równaniu, które da ci podpis cyfrowy. Sama sygnatura jest podzielony na dwie części, nazywane T i S. Aby sprawdzić, czy podpis jest poprawny, potrzebujesz tylko klucza publicznego (ten punkt na krzywej, który został wygenerowany przy użyciu klucza prywatnego) i umieszczasz go w jeszcze innym magicznym równaniu z jedną częścią podpisu (S). Jeżeli plik został poprawnie podpisany kluczem prywatnym, w wyniku otrzymasz drugą część podpisu (R). Krótko mówiąc, podpis składa się z dwóch liczb, T i S, które generowane są za pomocą klucza prywatnego, w wyniku czego możesz zastosować równanie matematyczne wykorzystujące klucz publiczny i S, co ostatecznie da T, dowodząc, że podpis jest ważny. Nie ma natomiast sposobu, aby poznać klucz prywatny lub utworzyć podpis przy użyciu tylko klucza publicznego.

Mam nadzieję, że teraz temat jest dla ciebie bardziej zrozumiały. Jeżeli nadal masz obawy, zerknij do artykułu An introduction to elliptic curve cryptography oraz A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography, które dosyć dokładnie i prosto wyjaśniają koncepcję krzywych eliptycznych. Polecam także Why Are They Called „Elliptic” Curves?. Natomiast jeśli chcesz pogłębić swoją wiedzę dotyczącą obu rodzajów kryptografii, polecam świetną prezentację pod tytułem ECC vs RSA: Battle of the Crypto-Ninjas. Przy okazji warto zapoznać się z dokumentami Standards for Efficient Cryptography Group.

Główny problem: ochrona klucza prywatnego #

Moim zdaniem, największym wyzwaniem w przypadku kryptografii asymetrycznej jest odpowiednie zarządzanie (zabezpieczenie) kluczami prywatnymi. Jest to znacznie ważniejsze niż rozważania na temat rozmiaru takich kluczy, mimo tego, że jest to oczywiście również kluczowy parametr, na którym opiera się bezpieczeństwo każdego z rozwiązań. Zazwyczaj administratorzy i developerzy wkładają dużo wysiłku w ochronę swoich kluczy prywatnych CA, ale dużo mniej wysiłku w ochronę kluczy prywatnych serwera HTTP (ponieważ taki serwer potrzebuje do nich dostępu przez cały czas, zwłaszcza jeśli serwer zostanie ponownie uruchomiony).

Kontrola kluczy prywatnych staje się trudna, ponieważ powinny być one maksymalnie bezpieczne, a dostęp do nich jak najbardziej ograniczony. Z drugiej strony, bezpieczeństwo jest ważne, jednak ja zawsze preferuję podejście racjonalnego bezpieczeństwa. Dlatego uważam, że w przypadku kluczy prywatnych należy zacząć od podstawowych kroków, które pozwolą zminimalizować ryzyko ich odczytania. Wszelkie niestandardowe propozycją mogą być ciekawe (tj. skrypty automatyzujące, przechowywanie kluczy na zdalnym zasobie), jednak pamiętaj, że przesuwa to kwestię bezpieczeństwa gdzie indziej, zwiększając dodatkowe możliwości pomyłki w implementacjach oraz tworząc nowe wektory potencjalnego ataku.

Tak naprawdę zapewnienie bezpieczeństwa kluczy prywatnych powinno iść w parze z odpowiednim ich rozmiarem oraz parametrami wykorzystywanymi podczas zestawiania sesji SSL/TLS. Polecam przeczytanie dokumentu Secure Distribution of SSL Private Keys with NGINX w celu zminimalizowania ew. ataku na klucze prywatne obsługiwane z poziomu serwera NGINX. Myślę, że w przypadku pozostałych technologii można kierować się podobnymi zaleceniami.

Możemy zacząć od tego, że dane prywatne, w tym wypadku klucz, muszą być chronione za pomocą odpowiednich uprawnień (np. list kontroli ACL) w systemie operacyjnym. Należy maksymalnie zminimalizować dostęp do takich kluczy prywatnych. Myślę, że należy tutaj podejść do tematu dość restrykcyjnie i uprawnienia na poziomie 0600 lub nawet 0400 dla plików oraz 0700 dla katalogów powinny być odpowiednie. Dobrym pomysłem jest także szyfrowanie katalogu lub całego systemu plików, na którym umieszczone są klucze prywatne. Pojawiają się tutaj jednak pytania, w jaki sposób i kiedy odszyfrować taki zasób, np. w przypadku usług, takich jak serwery HTTP, które wykorzystują klucze prywatne.

Ponadto uważam, że klucze prywatne dobrze jest chronić za pomocą hasła. Ważną kwestią jest jednak to, że hasło dotyczy przechowywania: kiedy klucz prywatny ma być użyty, najpierw jest odszyfrowywany w pamięci, a następnie wykorzystywany jest w postaci niezaszyfrowanej. Ustawienie hasła zminimalizuje możliwość ich odczytania w przypadku włamania na serwer i kradzieży, jednak nie chroni przed oczytaniem kluczy z pamięci serwera. Ponadto należy zapewnić odpowiednie mechanizmy przekazania haseł do danej usługi, w celu zdekodowania klucza, co może być problematyczne. Dobrze jest taki proces zautomatyzować lub wybrać usługę, która będzie miała zaimplementowane mechanizmy obsługi haseł (wielu haseł do wielu kluczy), np. poprzez odczytanie ich z pliku na serwerze. Plik taki oczywiście należy szczególnie chronić, można go szyfrować, jednak i tak będzie trzeba go rozszyfrować na pewien czas, aby odczytać hasła (proces ten także można zautomatyzować).

Bardzo istotnym czynnikiem jest także określenie jasnego i spójnego procesu, który określa, kto otrzymuje dostęp i jak/kiedy ten dostęp jest zabierany, np. gdy użytkownik opuszcza projekt lub firmę. Jeśli ktoś ma wystarczający dostęp do serwera, aby odczytać klucz, najprawdopodobniej ma również wystarczający dostęp, aby podłączyć debugger i pobrać klucz z pamięci. Posiadanie procesu nie zawsze jest wystarczającą ochroną. Musimy monitorować i sprawdzać, czy proces faktycznie działa. Ważne jest, aby okresowo sprawdzać, kto ma dostęp do kluczy prywatnych oraz czy proces przyznawania dostępu działa odpowiednio dobrze. Czasami ludzie opuszczają projekty lub firmę, ale ich konta użytkowników nadal mają dostęp do kluczy prywatnych. Zminimalizowanie liczby użytkowników, którzy mają dostęp do kluczy prywatnych, jest również bardzo, bardzo ważne.

W przypadku serwerów HTTP, a zwłaszcza środowisk rozproszonych, pojawia się kolejny problem: w jaki sposób przechowywać takie klucze? W takiej sytuacji chyba najlepszym rozwiązaniem jest wygenerowanie i przechowywanie kluczy prywatnych w lokalnym systemie plików. Myślę, że kluczowe znaczenie ma to, aby generowanie klucza odbywało się w tym samym systemie i tym samym lokalnym systemie plików, co lokalizacja przechowywania. Można oczywiście przechowywać klucze na zaszyfrowanej pamięci USB lub zdalnym zasobie, który będzie montowany na każdej maszynie. W tym drugim przypadku pojawiają się następne problemy: w jaki sposób zapewnić montowanie? Co jeśli punkt, na którym znajduję się wszystkie klucze prywatne i są one współdzielone, ulegnie awarii? Wygenerowanie klucza na serwerze, a następnie przesłanie go z powrotem do systemu lokalnego i przechowywanie go tylko dodaje kolejne punkty podatności. Dlaczego miałbyś chcieć zwiększyć ryzyko złamania klucza prywatnego? Moim zdaniem (należy jednak podejść do tego indywidualnie) klucze prywatne nigdy nie powinny być przesyłane przez sieć i nigdy nie powinny być przechowywane w innym systemie.

Oczywiście temat jest bardzo szeroki i należy dosyć dokładnie go zbadać. Podsumowując, uważam, że podstawowymi i bardzo rozsądnymi krokami są:

Niestety jesteśmy tutaj trochę na straconej pozycji, ponieważ nie ma idealnego rozwiązania, które pozwoliłoby w pełni zabezpieczyć klucze prywatne. Zdecydowanie jednak powinniśmy skupić się na racjonalnie bezpiecznym rozwiązaniu w przeciwieństwie do prostoty. Na koniec polecam zapoznać się z poniższymi zasobami:

A co z wydajnością? #

Czysto asymetryczne szyfrowanie jest znacznie wolniejsze niż szyfrowanie symetryczne (takie jak DES lub AES), dlatego w celu rozwiązania tych problemów używana jest tzw. kryptografia hybrydowa (mieszana), w której kosztowne operacje klucza publicznego (RSA/ECC) wykonywane są tylko w celu zaszyfrowania i wymiany (tutaj jak już wiemy, wykorzystuje się wymianę kluczy Diffie-Hellman) klucza tymczasowego dla algorytmu symetrycznego, który to jest używany do zaszyfrowania prawdziwej wiadomości. Takie mieszane rozwiązanie zapewnia możliwość stosowania szybkich, symetrycznych algorytmów, takich jak AES (które mają najczęściej wsparcie sprzętowe), używanych do ochrony samego komunikatu, oraz wolniejszych, asymetrycznych algorytmów, takich jak RSA, które to są z kolei używane do ochrony kluczy wymaganych przez algorytmy symetryczne.

Takie połączenie obu technik oferowane przez standardowe schematy kryptograficzne, takie jak TLS i PGP (ang. Pretty Good Privacy), nakłada stały koszt wydajności na każdą wiadomość lub sesję. Jak duży jest to wpływ, zależy od wybranych algorytmów i wykonywanych operacji.

Zacznijmy jednak od początku (przy okazji przypomnimy sobie parę rzeczy, które już były omawiane). Na podstawie znajomości klucza publicznego, nie powinno być możliwe odtworzenie (obliczenie) klucza prywatnego, jednak klucz publiczny może być wyznaczony (wyodrębniony) z klucza prywatnego (na tym polega w założeniu kryptografia klucza publicznego, czyli aby wygenerowanie klucza prywatnego na podstawie klucza publicznego było jak najtrudniejsze obliczeniowo). Zawsze to było dla mnie niejasne (biorąc pod uwagę źródła, które pomagały mi zrozumieć ten temat), ponieważ uważam, że w przypadku algorytmu RSA należy zrozumieć jeden ważny fakt: w teorii zawsze można złamać ten typ klucza, obliczając czyjś klucz prywatny z jego klucza publicznego — czyli gdy jesteśmy w stanie rozłożyć moduł (liczbę n, która jest wspólna zarówno dla klucza publicznego, jak i prywatnego) na dwa czynniki pierwsze. Jeżeli osoba podsłuchująca potrafiłaby to zrobić w rozsądnym czasie (tzn. liczbę n rozłożyć na iloczyn pq), system zostałby złamany.

Możliwość wyliczenia klucza prywatnego RSA z publicznego jest jednak ograniczona długością modułu, ponieważ jeśli jest on wystarczająco duży, nawet jeśli będzie można przeprowadzić rozkład na czynniki, nie będzie to wykonalne (będzie nieefektywne), co oznacza tyle, że ​​czas (czyli główna miara wydajności danego algorytmu) będzie zbyt długi oraz moc obliczeniowa potrzebna do tego jest po prostu niewystarczająca. Oczywiście stwierdzenie, że nie da się wyliczyć klucza prywatnego z publicznego, jest moim zdaniem jak najbardziej prawdziwe. Należy pamiętać, że klucz prywatny wykorzystujący algorytm RSA nie składa się tylko z modułu i wykładnika publicznego, zazwyczaj zawiera on jeszcze inne komponenty. Idąc za tym, warto przyjrzeć się strukturze takiego klucza prywatnego, która została zdefiniowana w RFC 3447 [IETF], aby lepiej zrozumieć to, co przed chwilą napisałem:

-----BEGIN RSA PRIVATE KEY-----
RSAPrivateKey ::= SEQUENCE {
  version           Version,
  modulus           INTEGER,  -- n
  publicExponent    INTEGER,  -- e
  privateExponent   INTEGER,  -- d
  prime1            INTEGER,  -- p
  prime2            INTEGER,  -- q
  exponent1         INTEGER,  -- d mod (p-1)
  exponent2         INTEGER,  -- d mod (q-1)
  coefficient       INTEGER,  -- (inverse of q) mod p
  otherPrimeInfos   OtherPrimeInfos OPTIONAL
}
-----END RSA PRIVATE KEY-----

W tym samym dokumencie opisano także strukturę klucza publicznego RSA:

-----BEGIN RSA PUBLIC KEY-----
RSAPublicKey ::= SEQUENCE {
  modulus           INTEGER,  -- n
  publicExponent    INTEGER   -- e
}
-----END RSA PUBLIC KEY-----

Natomiast format kluczy prywatnych ECC został dokładnie zdefiniowany w RFC 5915 [IETF] i wygląda następująco:

-----BEGIN EC PRIVATE KEY-----
ECPrivateKey ::= SEQUENCE {
  version        INTEGER { ecPrivkeyVer1(1) } (ecPrivkeyVer1),
  privateKey     OCTET STRING,
  parameters [0] ECParameters  OPTIONAL,
  publicKey  [1] BIT STRING OPTIONAL
}
-----END EC PRIVATE KEY-----

Informację dotyczącą formatu klucza publicznego dla tego algorytmu znajdziesz w RFC 5480 - 2.2. Subject Public Key [IETF].

Widzimy, że klucz prywatny RSA wygenerowany przy użyciu polecenia openssl zawiera elementy zarówno klucza publicznego, jak i prywatnego, oraz kilka dodatkowych składników. Kiedy generujesz/wyodrębniasz/wyprowadzasz klucz publiczny z klucza prywatnego, openssl kopiuje dwa z tych składników (e, n) do oddzielnego pliku, który staje się kluczem publicznym.

Co również istotne, każda asymetryczna para kluczy jest unikatowa, dzięki czemu wiadomość zaszyfrowana przy użyciu klucza publicznego może zostać odczytana tylko przez serwer/osobę posiadającą odpowiedni klucz prywatny. Tak samo w drugą stronę, dane podpisane za pomocą klucza prywatnego można zweryfikować tylko za pomocą klucza publicznego. Przedstawione to zostało na poniższej grafice:

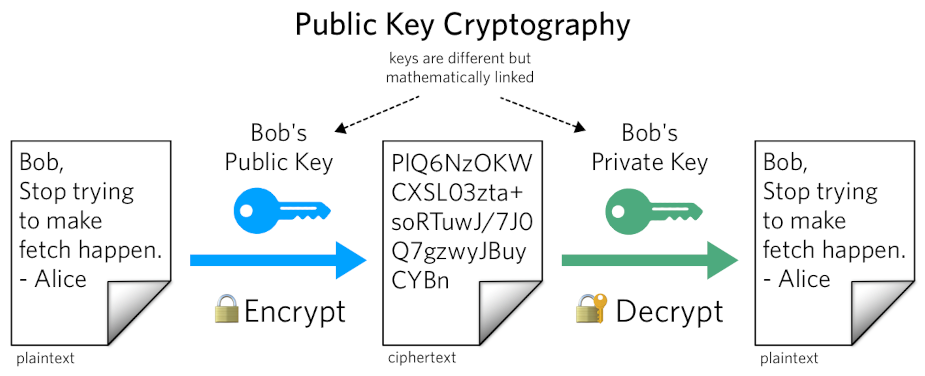
Możesz zapytać, na co nam te początkowe dywagacje? Jak widzisz, klucz publiczny jest w pewien sposób powiązany z kluczem prywatnym, co oznacza, że musi istnieć między nimi jakaś unikalna (matematyczna) zależność. W związku z tym może to być słaby punkt, który przy jego złamaniu, może doprowadzić do kompromitacji szyfrowania.

Jeżeli klucz prywatny zostanie udostępniony lub w jakikolwiek sposób ujawniony, bezpieczeństwo wszystkich wiadomości, które zostały zaszyfrowane za pomocą odpowiadającego mu klucza publicznego, zostanie naruszona.

Narzut obliczeniowy jest wtedy dość oczywisty, ponieważ klucz publiczny jest dostępny dla każdego, stąd musi być (wraz z kluczem prywatnym) wystarczająco długi, aby zminimalizować możliwość jego złamania (aby był poza zasięgiem możliwości przeprowadzenia faktoryzacji nawet największych superkomputerów na świecie). W innym wypadku, ujawnienie klucza publicznego atakującemu naraziłoby klucz prywatny, zwłaszcza gdybyśmy użyli rozmiarów porównywalnych z szyfrowaniem symetrycznym.

Rezultatem jest znacznie silniejszy poziom szyfrowania. Koniec końców, 128-bitowy klucz symetryczny (np. AES) i 2048-bitowy klucz asymetryczny (np. RSA) oferują mniej więcej podobny poziom bezpieczeństwa. Wydajność jest tutaj jednym z głównych kryteriów doboru odpowiednich rozmiarów kluczy. Mniejsze klucze mają szybsze algorytmy generowania sygnatur, ponieważ matematyka, która leży u ich podstaw, obejmuje mniejsze liczby. Mniejsze klucze publiczne oznaczają mniejsze certyfikaty i w konsekwencji mniej danych do przekazania w celu ustanowienia połączenia SSL/TLS — oznacza to szybsze połączenia i krótsze czasy ładowania witryn internetowych, ponieważ skraca czas potrzebny do wykonania uzgadniania.

W przypadku kluczy RSA każde podwojenie długości powoduje, że odszyfrowywanie jest kilka razy (nawet 6-7 razy) wolniejsze. Oczywiście długość klucza wpływa również na szybkość szyfrowania, ale zwykle bardziej należy martwić się o szybkość deszyfrowania, ponieważ raz, że jest to część, która ma miejsce na serwerze, a dwa, że deszyfrowanie jest znacznie wolniejsze niż szyfrowanie ze względu na wykładnik potęgi, który jest ogromny. Poza tym, w przypadku RSA operacje deszyfrowania i podpisywania są stosunkowo wolne, ponieważ wymagają modularnego potęgowania z dużym wykładnikiem prywatnym. Z drugiej strony, szyfrowanie RSA i weryfikacja podpisu są bardzo szybkie, ponieważ wykorzystują mały wykładnik publiczny (ta różnica zmienia się wraz z długością klucza).

Jeśli użyjesz modułu o rozmiarze 4096-bit, proces deszyfracji bloku danych może zająć około sekundy czasu procesora (oczywiście zależy od jego typu oraz częstotliwości, obecne mikroprocesory radzą sobie z tym lepiej) i należy mieć świadomość, że jest to ogromny czas (zwłaszcza gdy zostanie połączony z dodatkowymi danymi, które są wykorzystane podczas sesji SSL/TLS), jaki jednostka centralna musi poświęcić na ten proces. Pamiętaj, że procesor zazwyczaj ma jeszcze wiele innych zadań do wykonania, a sam czas, jaki jest przydzielany na te zadania, zazwyczaj określany jest w milisekundach. Na przykład atakujący może efektywnie wykorzystać sekundę czasu procesora na naszym serwerze, wysyłając do niego losowe dane i powodując znaczne wykorzystanie procesora (a może i nawet zawieszenie całego serwera). Przy długości klucza 1024-bit, odszyfrowanie zajmuje kilkadziesiąt milisekund, więc problem ten jest znacznie zniwelowany.

Poniżej znajduje się porównanie wydajności najczęściej stosowanych rozmiarów kluczy RSA z perspektywy klienta:

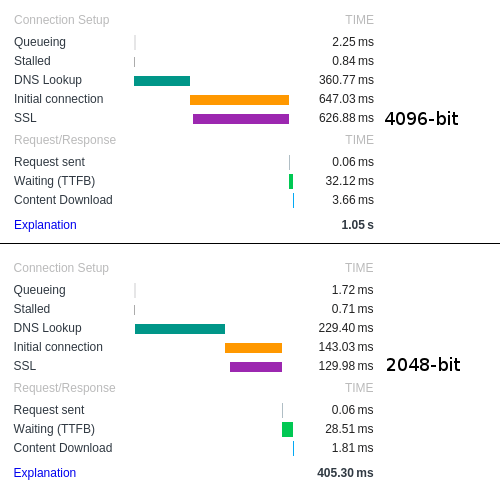
Oczywiście istnieje wiele innych dodatkowych czynników, które mogą wpływać na „szybkość” infrastruktury klucza publicznego. Ponieważ jednym z problemów związanych z tym systemem jest zaufanie, większość problemów implementacji dotyczy urzędów certyfikacji (CA), które są podmiotami ufającymi w delegowaniu par kluczy i sprawdzaniu ich tożsamości.

Spójrz także na porównanie dla RSA 2048-bit i 4096-bit, a także dla ECDSA P-224 oraz P-256. W ostatnim przykładzie przetestowano także EdDSA Ed25519:

openssl speed rsa2048 rsa4096 ecdsap224 ecdsap256

                  sign    verify    sign/s verify/s
rsa 2048 bits 0.001967s 0.000057s    508.5  17499.1
rsa 4096 bits 0.014144s 0.000251s     70.7   3977.9

                  sign    verify    sign/s verify/s
224 bit ecdsa   0.0001s   0.0002s   8968.9   4443.7
256 bit ecdsa   0.0001s   0.0002s  12423.0   5128.8

OpenSSL 1.1.0j 20 Nov 2018 24 x Intel(R) Xeon(R) CPU X5675 @ 3.07GHz

openssl speed rsa2048 rsa4096 ecdsap224 ecdsap256

                  sign    verify    sign/s verify/s
rsa 2048 bits 0.000940s 0.000028s   1064.0  35089.4
rsa 4096 bits 0.006109s 0.000093s    163.7  10706.8

                  sign    verify    sign/s verify/s
224 bit ecdsa   0.0001s   0.0002s   9738.3   4467.7
256 bit ecdsa   0.0001s   0.0001s  16187.7   7279.2

OpenSSL 1.1.0j 20 Nov 2018; 32 x Intel(R) Xeon(R) CPU E5-2620 v4 @ 2.10GHz

openssl speed rsa2048 rsa4096 ecdsap224 ecdsap256

                  sign    verify    sign/s verify/s
rsa 2048 bits 0.000641s 0.000020s   1559.2  50436.5
rsa 4096 bits 0.004314s 0.000069s    231.8  14415.6

                  sign    verify    sign/s verify/s
224 bit ecdsa   0.0001s   0.0002s  14001.0   6141.8
256 bit ecdsa   0.0000s   0.0001s  25426.6   9625.4

OpenSSL 1.1.0l 10 Sep 2019; 64 x Intel(R) Xeon(R) Silver 4216 CPU @ 2.10GHz

openssl speed rsa2048 rsa4096 ecdsap224 ecdsap256 ed25519

                  sign    verify    sign/s verify/s
rsa 2048 bits 0.000696s 0.000023s   1436.6  42885.2
rsa 4096 bits 0.005432s 0.000082s    184.1  12151.1

                  sign    verify    sign/s verify/s
224 bits ecdsa  0.0005s   0.0004s   1947.9   2307.8
224 bits ecdsa  0.0000s   0.0001s  33991.2  12539.6

                  sign    verify    sign/s verify/s
253 bits EdDSA  0.0000s   0.0001s  23021.1   7091.0

OpenSSL 1.1.1d-freebsd 10 Sep 2019 16 x Intel(R) Xeon(R) Silver 4112 CPU @ 2.60GHz

Z powyższych zrzutów widzimy, że ECDSA jest nieporównywalnie szybszy podczas podpisywania niż RSA, ale wolniejszy podczas weryfikacji. Wydajność RSA spada bardzo szybko wraz ze wzrostem rozmiaru klucza, podczas gdy spadek dla ECDSA jest delikatniejszy. W obu przypadkach tak naprawdę czas wymagany do wykonania operacji się wydłuża, jednak dla RSA dzieje się tak ze względu na większe zabezpieczenia, natomiast dla ECDSA czasy rosną w znacznie wolniejszym tempie. ECC jest znacznie szybszy niż RSA podczas generowania kluczy. Znalezienie dużych liczb pierwszych dla RSA jest trudnym zadaniem, nawet dla obecnych procesorów, biorąc pod uwagę wystarczająco duży rozmiar klucza.

Możemy wyciągnąć ciekawy wniosek, który będzie odpowiedzią na pytanie, który z rodzajów kluczy jest lepszy. Oczywiście to zależy. Jeżeli planujesz wykonywać bardzo dużo podpisów, powinieneś wybrać ECDSA. Natomiast jeśli planujesz przeprowadzać wiele weryfikacji, powinieneś użyć RSA. Jest to oczywiście podejście zero-jedynkowe, które ni jak sprawdza się w codziennym, produkcyjnym życiu. Co istotne, korzystanie z kluczy ECDSA wymaga więcej pracy obliczeniowej w przeglądarce klienta. Jednak nawet w porównaniu z 2048-bitowym kluczem RSA badania wykazały (zerknij na pracę An Experimental Study of TLS Forward Secrecy Deployments), że nie ma ogólnej utraty wydajności. Niezależnie od wyboru, w pierwszej kolejności powinniśmy skupić się na minimalnym rozmiarze kluczy (tak, aby uzyskać poziom, powyżej którego będziemy bezpieczni) oraz zapewnić ochronę kluczy prywatnych, co nie jest wcale takim łatwym zadaniem. Generalnie użycie certyfikatu ECDSA zmniejsza koszt działania klucza prywatnego prawie dziesięć razy, oszczędzając zasoby sprzętowe, w tym cykle procesora.

Pamiętajmy, że ECDSA zależy w dużej mierze od generatora liczb losowych. Zła jakość takiego generatora może naruszyć klucz prywatny ECDSA a dwa, prędkości tego algorytmu mogą być mniejsze, jeśli np. generator blokuje się z jakiegoś powodu.

Jeżeli dobrze przyjrzałeś się powyższym testom, to rzuciła się tobie w oczy na pewno jedna rzecz: dlaczego w każdym z przypadków ecdsap256 jest szybszy niż ecdsap224? Nie powinno być odwrotnie? Obie krzywe mają podobny kształt i podobne liczby pierwsze bliskie potęgom dwójki, więc nie ma tak naprawdę dużych różnic w wydajności. Jednak w praktyce różne implementacje będą miały różną wydajność, a niektóre krzywe będą lepiej zoptymalizowane (patrz: Fast Elliptic Curve Cryptography in OpenSSL). Aby być na bieżąco z wszelkiego rodzaju poprawkami czy optymalizacjami implementacji danej krzywej, warto przeglądać listę zmian między wersjami biblioteki OpenSSL.

Wracając do porównania między RSA a ECC, jedyną potwierdzoną naukowo przewagą RSA nad kryptografią krzywych eliptycznych jest to, że operacje na kluczu publicznym (np. weryfikacja podpisu, w przeciwieństwie do generowania podpisu) są szybsze dzięki RSA (co potwierdza też powyższy zrzut). Pamiętajmy jednak, że operacje z kluczem publicznym rzadko są wąskim gardłem. W dokumencie Architectural evaluation of algorithms RSA, ECC and MQQ in ARM processors [PDF] porównano i omówiono wydajność obu typów kryptografii asymetrycznej. Polecam zapoznać się także ze świetną analizą porównawczą RSA i ECC opracowaną w dokumencie RSA and ECC: A Comparative Analysis [PDF]. Eksperymenty w nim przedstawione przeprowadzono w celu znalezienia upływu czasu (różnic w pomiarze czasu) podczas szyfrowania i deszyfrowania przez oba typy kryptografii na trzech próbnych danych wejściowych, tj. 8 bit, 64 bit i 256 bit, z losowymi kluczami na podstawie wytycznych NIST. Wykazały one, że ECC przewyższa RSA pod względem wydajności operacyjnej i bezpieczeństwa przy niższych parametrach. Autorzy wyciągnęli wniosek, że ECC jest szczególnie odpowiednie w przypadku systemów o ograniczonych zasobach.

Spójrzmy jeszcze na poniższy wykres porównujący obecnie stosowane rozwiązania:

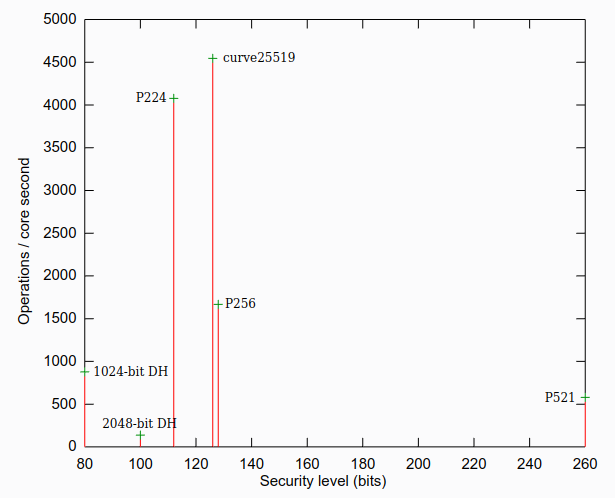
Pochodzi on z artykułu What a difference a prime makes.

Przy okazji zacytuję Adama Langley’a, autora bloga, z którego pochodzi powyższy wykres (o niektórych rodzajach krzywych pomówimy w dalszych rozdziałach):

P224 and P256 are not, fundamentally, very different. However, P256 has a nasty prime formation, as I explained previously, which kills the speed. Sadly, if you want to support the existing fleet of browsers, P256 is your fastest option.

Na koniec polecam także przestudiować świetną pracę inżynierów firmy Symantec: Elliptic Curve Cryptography (ECC) Certificates Performance Analysis [PDF]. Dostarcza ona świetną dokumentację na temat certyfikatów SSL/TLS opartych na krzywej eliptycznej, z naciskiem na porównanie z wszechobecnymi certyfikatami opartymi na RSA.

Pozostałe problemy #

Wydajność, o której powiedzieliśmy, jest tylko jednym z problemów. Musimy też pamiętać o kilku innych, równie ważnych kwestiach. Na przykład, operacje kryptograficzne oparte na kryptografii z kluczem publicznym nie są przeznaczone do szyfrowania surowych danych, tutaj znacznie lepiej spisują się algorytmy symetryczne. Dwa, jeśli chcesz zaszyfrować coś większego niż rozmiar kluczy RSA, musisz użyć ponownie szyfrowania symetrycznego, ponieważ szyfrowanie asymetryczne nie może szyfrować niczego większego niż jego własny rozmiar klucza.

Dla protokołu SSL/TLS, dodatkowe obciążenie narzucane przez asymetryczne algorytmy kryptograficzne w porównaniu z algorytmami symetrycznymi jest stałe — nie zależy od rozmiaru danych, tylko od rozmiarów kluczy, ponieważ szyfrowanie asymetryczne stosujemy do zaszyfrowania klucza symetrycznego, a następnie szyfrowanie symetryczne tym kluczem do zaszyfrowania faktycznych danych.

Pamiętajmy też, że klucz publiczny nie działa bez infrastruktury zarządzania kluczami. Jeśli nie mamy schematu weryfikacji kluczy publicznych, atakujący mogą zastąpić prawdziwe klucze własnymi parami kluczy, aby przeprowadzić ataki typu man-in-the-middle (dlatego też jest to jeden z powodów przejścia kluczy asymetrycznych przez rygor certyfikatów).

Ponadto kryptografia asymetryczna jest podatna na więcej luk w implementacji niż AES. Na przykład obie strony muszą uzgodnić odpowiednie parametry, które są liczbami. Co jeśli atakujący w jakiś sposób będzie miał wpływ na te wartości? Innym przykładem jest luka w zabezpieczeniach RSA o nazwie Forgery Attack Against RSA Digital Signature, która wystąpiła w wielu zaawansowanych implementacjach SSL/TLS. Kryptografia oparta na krzywych eliptycznych także może posiadać pewne słabości, spójrz na dokumenty Trapping ECC with Invalid Curve Bug Attacks [PDF], Degenerate Curve Attacks [PDF] oraz To Infinity and Beyond: Combined Attack on ECC Using Points of Low Order [PDF].

Generalnie, jeśli chodzi o szyfrowanie danych w spoczynku, np. poczty czy dokumentów, tutaj zaleceniem jest stosowanie PGP, które jest uważane za bezpieczne i w większości wolne od głupich błędów implementacyjnych. Natomiast w przypadku danych, które zmieniają się w czasie rzeczywistym, lepiej stosować protokołu SSL/TLS, który jest globalnie stosowanym i sprawdzonym standardem.

Co znaczy, że klucz jest N-bitowy? #

Pamiętaj, że kiedy mówimy o dużych, bądź nawet bardzo dużych liczbach, to naprawdę tak jest. Obecne implementacje RSA mogą używać np. 4096-bitowej liczby dla n. Obecnie nie jest znany sposób, w jaki dałoby się w rozsądnym czasie wyliczyć liczby o takiej wielkości, więc przy spełnieniu tego warunku RSA wydaje się całkiem bezpieczny (z drugiej strony, nie udało się także udowodnić, że jest to niemożliwe, myślę, że komputery kwantowe mogą zweryfikować pogląd bezpieczeństwa kluczy RSA o takim oraz większym rozmiarze).

Generalnie, kiedy widzisz N-bitowy klucz RSA, oznacza to, że moduł (liczba n, która jest dzielona przez klucze publiczny i prywatny) ma długość N-bitów. W RSA bierzemy dwie liczby pierwsze (p i q), a następnie mnożymy je razem, aby uzyskać moduł n. Wartość modułu, będąca cyfrą dziesiętną wygenerowaną z dwóch N-bitowych liczb pierwszych, jest wtedy częścią klucza publicznego i prywatnego. Dla rsa2048 używamy dwóch 1024-bitowych liczb pierwszych, zaś dla rsa4096 używamy dwóch 2048-bitowych liczb pierwszych. Jeżeli mówimy, że klucz RSA ma długość, np. 2048-bit, to tak naprawdę oznacza, że ​​wartość modułu wynosi od 22047 do 22048. Ponieważ klucz publiczny i prywatny danej pary mają ten sam moduł, z definicji mają one również tę samą długość. Liczby pierwsze powinny mieć długości zbliżone.

Znalezienie dwóch liczb pierwszych jest uciążliwą procedurą, jednak wykonuje się ją tylko w celu stworzenia nowej pary kluczy. Natomiast przy szyfrowaniu i deszyfrowaniu oblicza się jedynie potęgi liczb całkowitych. Tutaj znajdziesz bardzo prosty skrypt napisany w pythonie, za pomocą którego można wygenerować dwie losowe liczby pierwsze (p i q) o określonej długości. Następnie za pomocą metody RSA znajdowany jest moduł (n) oraz zwrócona zostaje liczba cyfr dziesiętnych tych wartości.

Musisz wiedzieć, że typowe rozmiary kluczy RSA to 1024, 2048 lub 4096 bitów. Wiemy już, że liczba ta jest liczbą bitów w module lub inaczej mówiąc, jest to długość modułu użytego do obliczenia pary kluczy RSA (klucz publiczny składa się z modułu i wykładnika publicznego, natomiast klucz prywatny składa się z modułu i wykładnika prywatnego). Liczby te są wybierane przez jakiś losowy proces.

Rozmawiając o rozmiarach kluczy, należy wspomnieć o sile określonego algorytmu szyfrowania. Mówiąc ogólnie, siła to liczba prób, które należy podjąć, aby złamać dany algorytm. Dokładniej, siła to ilość obliczeń, które trzeba wykonać, aby znaleźć dany sekret. Aby określić siłę algorytmu kryptograficznego, można powiązać z nim poziom bezpieczeństwa, zwykle wyrażany jako liczba bitów. Ta liczba bitów koreluje z minimalnym wysiłkiem, jaki jest potrzebny, aby złamać kryptogram obliczony przez ten algorytm. Zwykle algorytmy klucza symetrycznego, które są w powszechnym użyciu, mają zabezpieczenia równe długości klucza. Jednak nie są znane żadne algorytmy klucza asymetrycznego z tą właściwością (najbliższa temu jest kryptografia oparta na krzywej eliptycznej).

Złamanie algorytmów z kluczem publicznym nie wymaga wypróbowania każdego możliwego klucza tak jak w przypadku algorytmów symetrycznych, gdzie dla 8-bitowego klucza istnieje 256 możliwych prób jego złamania (oczywiście istnieje szansa znalezienia klucza po połowie prób), natomiast już dla klucza o długości 128-bit zajmie to 1025 lat (wiek wszechświata datowany jest na 1010 lat, więc widzisz, że łamanie 128-bitowych kluczy metodą brute force nie jest zbyt praktyczne). Dlaczego? Złamanie tych algorytmów wymaga próby uwzględnienia dużej liczby lub wzięcia dyskretnych logarytmów w bardzo dużym polu skończonym w przypadku krzywych eliptycznych.

Dla RSA podobnie jak w przypadku kluczy symetrycznych, ataki na, powiedzmy, 2048-bitowe klucze polegają jednak na wypróbowaniu wszystkich (dostępnych) kluczy o określonym rozmiarze, ale w przeciwieństwie do klucza symetrycznego nie każda liczba 2048-bitowa jest kluczem RSA (ponieważ musi nią być iloczyn dwóch liczb pierwszych). Ponadto bezpieczeństwo RSA polega (częściowo) na fakcie, że łatwo jest wybrać dwie losowe liczby pierwsze, ale bardzo trudno jest je odkryć. Tak więc, chociaż przestrzeń klucza jest większa, w rzeczywistości jest mniej możliwych kluczy RSA dla dowolnej liczby bitów niż dla tego samego rozmiaru klucza symetrycznego, ponieważ istnieje skończona ilość liczb pierwszych o tej wielkości (ponadto mogą być mniejsze, ale nie większe).

Algorytm RSA może używać tylko par liczb pierwszych, podczas gdy w kryptografii symetrycznej można używać dowolnej liczby o tym samym rozmiarze. Wniosek z tego jest następujący: jeśli rozmiar klucza niezależnie od wykorzystanego algorytmu jest za mały, nie masz żadnego zabezpieczenia. Jeśli liczba bitów jest wystarczająco duża, masz zabezpieczenie przed całą mocą obliczeniową, jaka obecnie istnieje i biorąc pod uwagę dzisiejsze rozumienie matematyki. W idealnym świecie chodzi o to, że jedynym sposobem na włamanie się do połączenia sieciowego lub magazynu danych zabezpieczonego np. szyfrem symetrycznym jest wypróbowanie wszystkich kluczy.

Przy tej okazji i przed przejściem dalej, zapoznaj się z dwoma ciekawymi tematami odnoszącymi się do rozmiaru kluczy w obu rozwiązaniach: Security strength of RSA in relation with the modulus size i Why is the strength of an Elliptic Curve Cryptography (ECC) half the size of the prime field size?.

Krzywe eliptyczne i rozmiar klucza #

W przypadku kryptografii opartej na krzywych eliptycznych, każdy rozmiar bitu zapewnia więcej możliwości niż RSA, co sprawia, że ​​podejście wykorzystujące atak siłowy jest bardzo mało prawdopodobne. Więcej o tym rodzaju kryptografii przeczytasz w genialnej książce Handbook of Elliptic and Hyperelliptic Curve Cryptography [PDF]. Polecam także bardzo przystępną rozprawę doktorską wykonaną pod kierunkiem dr hab. Janusza Szczepańskiego prof. IPPT PAN: Wydajne metody generowania bezpiecznych parametrów algorytmów klucza publicznego [PDF], oraz bardzo ciekawą prezentację Elliptic Curve Cryptography Overview.

Ten rodzaj kryptografii zapewnia możliwość użycia znacznie mniejszych kluczy i podpisów cyfrowych, a także znacznie przyspiesza ich generowanie. Inną ogromną zaletą, związaną ze znacznie mniejszym rozmiarem, jest niższe wykorzystanie zasobów sprzętowych. Natomiast sam proces szyfrowania i deszyfrowania jest umiarkowanie szybki. Oczywiście to nie tak, że klucze RSA są tragicznie wolne, są również bardzo szybkie, zapewniając bardzo proste szyfrowanie i weryfikację oraz są łatwiejsze do wdrożenia, co jest ich ogromną zaletą.

Rozmiar, o którym mówimy w odniesieniu do krzywych eliptycznych, jest tzw. rozmiarem pola, na którym zdefiniowana jest krzywa eliptyczna. Ogólnie rzecz biorąc, krzywa ECC zaprojektowana dla pola N-bitowego będzie miała klucz N-bitowy. Mówiąc dokładniej, klucz prywatny jest generowany jako losowa liczba całkowita natomiast klucz publiczny to punkt na krzywej eliptycznej, obliczony przez mnożenie jej punktów, czyli klucza prywatnego i generatora (z góry określonego punktu na krzywej).

Spójrzmy jednak na przykłady. Krzywa Curve25519 jest 255-bitową krzywą eliptyczną i ma w rzeczywistości 252-bitowe klucze prywatne, chociaż są one zwykle kodowane jako 256-bitowe wartości z czterema stałymi bitami. Klucze publiczne są 256-bitowymi wartościami, ale zawierają tylko 255 bitów informacji, ponieważ ostatni bit ma zawsze wartość 0. Kolejny przykład to krzywa secp160r1, która używa 160-bitowego pola. W tym wypadku x i y mogą mieć długość do 160 bitów więc (x, y) wynosi 320 bitów. Zgodnie z tym, klucz prywatny to rzeczywiście 160-bitowa liczba całkowita zaś klucz publiczny to punkt na krzywej, zwykle reprezentowany przez współrzędne x, y (każda 160-bit) o łącznej długości 320 bitów. Wniosek z tego taki, że rozmiar pola niekoniecznie odpowiada rozmiarowi klucza.

W przypadku krzywej secp256k1 (więcej na jej temat do poczytania w artykule Bitcoin key mechanism and elliptic curves over finite fields) klucz prywatny to 256-bitowa liczba całkowita (32 bajty), a skompresowany klucz publiczny to 257-bitowa liczba całkowita (~33 bajty). Skompresowany, czyli? Skompresowany klucz to po prostu sposób na przechowywanie klucza publicznego w mniejszej liczbie bajtów (tutaj 33 bajty zamiast 65 bajtów). W przypadku skompresowanych kluczy publicznych tylko współrzędna x jest kodowana, natomiast współrzędna y może być wartością parzystą lub nieparzystą.

Widzimy, że skompresowana forma wymaga o połowę mniej miejsca + 1 bit określający parzystość bądź nieparzystość (mówiąc fachowo, jest to tzw. bit wskazujący, który określa położenie klucza publicznego, czyli punkty na krzywej, bardziej na lewo bądź na prawo wzdłuż nakreślonej krzywej). Kompresja klucza publicznego jest po prostu inną, w pełni kompatybilną i bezpieczną (są to dokładnie te same klucze) formą przechowywania, a jedynym kosztem takiego rozwiązania jest kilka dodatkowych obliczeń (np. dekompresja takiego klucza).

Zatrzymajmy się na chwilę. Czytając na temat krzywej Curve25519, która notabene jest jedną z najszybszych krzywych ECC, spotkasz się z różnym nazewnictwem, np. X25519, Ed25519 czy Edwards25519. Tak, jest to nieco zagmatwane (i sam niestety poczyniłem to w tym wpisie), zwłaszcza że pierwotnie X25519 nazywał się Curve25519, ale teraz Curve25519 oznacza po prostu krzywą eliptyczną, a X25519 oznacza kryptosystem (mam nadzieję, że mogę użyć takiego określenia), dlatego należy wyjaśnić, pomijając matematyczne technikalia, co jest dokładnie czym.

Po pierwsze, Curve25519 i Edwards25519 to krzywe eliptyczne na polu skończonym jednak o różnym kształcie — nie są dokładnie tym samym — opierają się na tej samej krzywej bazowej, ale używają różnych reprezentacji. Natomiast X25519 jest wysokowydajną funkcją zbudowaną na podstawie Curve25519 przeznaczoną do użytku ze schematem uzgadniania kluczy Diffie-Hellmana (ECDH) zaś Ed25519 to algorytm podpisu klucza publicznego (podobnie jak ECDSA) wykorzystujący krzywą Twisted Edwards, która oferuje bardzo szybkie podpisywanie i weryfikację podpisów oraz generowanie kluczy przy zachowaniu wysokiego poziomu bezpieczeństwa.

W takim razie podsumujmy:

Kończąc, są to dwa wysokowydajne algorytmy wykorzystujące jako podstawę krzywą Curve25519, w których Ed25519 używany jest do podpisywania a X25519 do wymiany kluczy (DH). Dokładne wyjaśnienie znajdziesz w odpowiedzi samego autora, Daniel Bernsteina: 25519 naming. Zachęcam także do zapoznania się z artykułem A Deep Dive into X25519 oraz odpowiedzią na pytanie Curve25519 over Ed25519 for key exchange? Why?.

Jeśli używasz ECDSA, który jest obecnie preferowanym schematem podpisu cyfrowego dla kryptografii krzywych eliptycznych, zalecany rozmiar klucza zmienia się w zależności od użycia (używanie różnych rozmiarów kluczy do różnych celów jest racjonalnym podejściem), patrz NIST 800-57-3 - Application-Specific Key Management Guidance (page 12, table 2-1) [NIST, PDF]. Generalnie 256-bitowy klucz ECC jest silniejszy niż 2048-bitowy klucz klasyczny (tak naprawdę równoważny temu rozmiarowi jest 224-bitowy klucz ECC). W miarę zwiększania wymaganego poziomu bezpieczeństwa przewaga przesuwa się jeszcze bardziej w kierunku ECDSA. Dzieje się tak dlatego, że aby zwiększyć poziom bezpieczeństwa, musisz zwiększyć rozmiar modułu RSA znacznie szybciej niż rozmiar krzywej ECDSA.

Wiele implementacji obsługuje ograniczoną liczbę krzywych, w której w większości w skład wchodzą krzywe P-256 i P-384 nazywane pakietem B (ang. Suite B) zdefiniowanym w RFC 5430 [IETF] zgodnie z zaleceniami NSA (definiuje on jednak znacznie więcej krzywych). Spotkałem się ze stwierdzeniem, aby używać krzywych P-384 lub P-521, a nie P-256 lub P-384 (jak wskazano w dokumencie NIST 800-57-3) ponieważ znajdują się znacznie poza ryzykowną strefą ich złamania (nie poddam jednak ocenie tej opinii).

NIST P-256 jest określany jako secp256r1 i prime256v1. Widzimy, że występuje tutaj różne nazewnictwo, jednak tak naprawdę możemy przyjąć, że wszystkie odnoszą się do tego samego. Natomiast istnieje pewna subtelna różnica między secp256k1 a secp256r1, która została wyjaśniona w artykule A tale of two elliptic curves. Dokładny spis krzywych znajdziesz w RFC 4492 - Appendix A. Equivalent Curves (Informative) [NIST].

Na koniec tego rozdziału jest jeszcze ważna rzecz warta wyjaśnienia. Powiedzieliśmy już kilkukrotnie o ECDSA, jednak co tak naprawdę oznacza ten termin? ECDSA jest algorytmem podpisu cyfrowego krzywej eliptycznej i służy do tworzenia cyfrowego podpisu danych, aby umożliwić weryfikację ich autentyczności. Co bardzo istotne, algorytm ten nie szyfruje danych i służy tylko i wyłącznie do podpisywania. W przypadku certyfikatu SSL certyfikat „krzywej eliptycznej” będzie używany tylko z podpisami cyfrowymi wykorzystując algorytm ECDSA. Myślę, że świetne wyjaśnienie znajdziesz w cytowanym już przeze mnie artykule Understanding How ECDSA Protects Your Data. Polecam także ECDSA: The digital signature algorithm of a better internet). Bardzo zachęcam do przeczytania obu, ponieważ przedstawiają proste i niezwykle ciekawe wyjaśnienie tego algorytmu.

Którą krzywą wybrać? #

Jak już się pewnie domyślasz, w przypadku krzywych eliptycznych, poziom bezpieczeństwa (siła kryptograficzna), wydajność (szybkość) oraz długość klucza zależy od zastosowanej krzywej. Niektóre z nich nie nadają się do zastosowań kryptograficznych ze względu na znane słabości (np. łatwość ich złamania, która powoduje, że szyfrowanie jest nieprzydatne, jeśli zbudowane zostanie o niewłaściwą krzywą).

Poniżej znajduje się lista najczęściej stosowanych krzywych eliptycznych:

W praktyce natomiast przeciętny klient obsługuje tylko dwie krzywe, te, które są wyznaczone z pakietu B:

Z tych dwóch typów najczęściej wykorzystywaną krzywą jest P-256, jednak coraz częściej wspieraną krzywą jest Curve25519. Co więcej, X25519 jest obecnie najczęściej używanym mechanizmem wymiany kluczy w TLSv1.3, a krzywa ta została przyjęta przez wiele znanych pakietów oprogramowania. Pamiętaj też, że użycie krzywej o większym rozmiarze klucza (pola) zwiększa koszty obliczeniowe i sieciowe.

Od czasu ujawnienia przez Edwarda Snowdena informacji dotyczących krzywych eliptycznych i NSA wiemy, że organizacja ta mogła manipulować standardami kryptograficznymi w celu włączenia backdoorów do tych algorytmów. Od tego czasu profesjonalni kryptografowie byli uzasadnienie podejrzliwi wobec systemu przedstawionego przez NIST i zgłaszali obawy dotyczące tych krzywych, głównie dlatego, że niektóre parametry zostały wybrane bez żadnego wyjaśnienia, a także dlatego, że krzywe zostały zaprojektowane przez NSA. Polecam zapoznać się z artykułem Assange, Snowden and the Trap Door oraz dwoma świetnymi dokumentami: Elliptic Curve Cryptography and Government Backdoors [PDF] i Selecting Elliptic Curves for Cryptography: an Efficiency and Security Analysis [PDF].

Problem z krzywymi NIST polega na odpowiedzi na pytanie, czy możemy ufać parametrom (ich losowości) tych krzywych. Cytując Bruce’a Schneiera (źródło): „Kryptografowie to konserwatywna grupa: nie lubimy używać algorytmów, które mają choćby ślad problemu”. Ponadto stwierdza on jednoznacznie (źródło):

„On the crypto bits in your guardian piece, I found especially interesting that you suggest classic discrete log crypto over ecc. I want to ask if you could elaborate more on that.” - I no longer trust the constants. I believe the NSA has manipulated them through their relationships with industry.

Dlatego myślę, że istnieje uzasadniona obawa ich stosowania, zwłaszcza że nie przedstawiono dobrego wyjaśnienia źródła zastosowanych parametrów, co może rodzić podejrzenia manipulacji standardami. Więcej o tym problemie poczytasz w artykule Suspect NIST crypto standard long thought to have a back door oraz w poście o tytule Should we trust the NIST-recommended ECC parameters?. Jednak aby być fair, zerknij także na Is there a feasible method by which NIST ECC curves over prime fields could be intentionally rigged?, który rzuca trochę inne światło na omawiany problem. Ze swojej strony rekomenduję wybór bezpiecznych krzywych dla kryptografii krzywych eliptycznych na podstawie zestawienia SafeCurves. Uważam, że powinno to być pierwsze źródło (albo jedno z podstawowych), z którego będziemy czerpać informacje o bezpieczeństwie krzywych eliptycznych, a także analizy sposobu ich porównywania w kontekście bezpieczeństwa (przy okazji zerknij na ciekawy artykuł The SafeCurves Scare: Why SafeCurves is a misnomer).

Wyżej wspomniałem o pewnych wątpliwościach co do stosowania krzywych z tego pakietu i jako alternatywę eksperci wskazują na stosowanie krzywej Curve25519 ze względu na wątpliwą jakość tych pierwszych oraz, co najważniejsze, na jej szybkość. NIST nie udokumentował jasno, dlaczego wybrał krzywe z pakietu B na korzyść istniejących alternatyw i tłumaczenia tej organizacji nie przekonały ekspertów zajmujących się kryptografią. Główną zaletą stosowania krzywej Curve25519 jest jej szybkość (jest szybsza, a nie silniejsza, ponieważ tak naprawdę każda z tych krzywych jest dość daleko w strefie, której nie można złamać), o której możesz poczytać w dokumencie Curve25519: new Diffie-Hellman speed records. Wiele implementacji przyspieszyło adopcję tej krzywej, która jest mniej podatna na błędy implementacji i jest przyjemną alternatywą dla wszystkich innych krzywych.

Co istotne, różnica szybkości w przypadku krzywych eliptycznych (głównie tych, które wymieniłem) jest raczej subtelna i w niektórych przypadkach trudną ją zauważyć, więc możemy przyjąć, że ogólnie wszystkie wyżej wymienione są szybkie i bezpieczne (jeśli ufamy NSA). Z drugiej strony, przewagą krzywych NIST jest zapewnienie lepszej interoperacyjności, ponieważ krzywe opracowane przez Daniela J. Bernsteina i Tanje Lange są znacznie nowsze i mniej rozpowszechnione. Zasadniczo wybór obecnie zależy od wsparcia po stronie serwera i klienta, a także pewnej estetyki, ponieważ niezależnie jakiego wyboru dokonasz i tak nie spowoduje on problemów z bezpieczeństwem — algorytmy kryptograficzne są najsilniejszą częścią całego systemu, a nie najsłabszą. Spotkałem się natomiast ze stwierdzeniem (co jest oczywiste, patrząc na standardy i zalecenia), żeby definitywnie nie używać krzywych secp112r1, secp112r2, secp128r1, secp128r2, secp160k1, secp160r1, secp160r2, secp192k1, ponieważ mają za mały rozmiar.

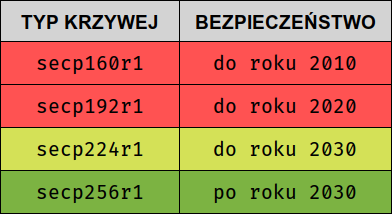
Z drugiej strony, wykonywanie operacji w oparciu np. o secp160r1 jest najszybsze, ale zapewnia niższy poziom ochrony niż w przypadku secp192r1, secp224r1 czy secp256r1.

Na tym moglibyśmy skończyć, jednak są jeszcze dwie, bardzo istotne kwestie, które muszę (ponownie) wyjaśnić i zrobię to w tym rozdziale — algorytm uwierzytelniania i algorytm wymiany kluczy, w tym wypadku oba oparte na kryptografii krzywych eliptycznych. Dlaczego o tym wspominam? Ponieważ algorytmy te są stosowane w różnych częściach standardu SSL/TLS — ECC może być używana zarówno w podpisach cyfrowych (do podpisywania i weryfikacji) za pośrednictwem Elliptic Curve DSA (ECDSA), jak i przy wymianie kluczy za pomocą Elliptic Curve Diffie-Hellman (ECDH lub ECDHE). Są to obecnie jedyne algorytmy krzywej eliptycznej obsługiwane przez OpenSSL. Po pierwsze, certyfikaty SSL można podpisywać za pomocą ECDSA zamiast RSA, który jest najczęściej stosowany. Drugie zastosowanie ECC ma miejsce podczas uzgadniania, gdy serwer i klient negocjują klucze sesji, które służą do szyfrowania wszystkich danych przesyłanych między serwerem a przeglądarką.

Wiemy już, że możemy mieć certyfikaty albo RSA, albo ECDSA (ECC). Algorytm uwierzytelniania ECDSA oznacza, że klucz prywatny oraz publiczny wykorzystują krzywą eliptyczną do wykonywania podpisów elektronicznych (w TLS do podpisywania wiadomości) — czyli określa, jaki algorytm wykorzystano do weryfikacji autentyczności serwera. Natomiast algorytm wymiany kluczy, tj. ECDHE lub ECDH (oba są odmianą Diffie-Hellman wykorzystującą krzywą eliptyczną, gdzie pierwszy to tzw. wersja efemeryczna z losowym kluczem, druga wykorzystuje stały klucz) decyduje o sposobie wymiany kluczy symetrycznych (taki uzgodniony klucz może zostać wykorzystany do szyfrowania komunikacji) — czyli określa, jaką kryptografię asymetryczną stosuje się do wymiany kluczy. Przykład: generujemy klucze ECDHE potrzebne do wymiany klucza symetrycznego. Następnie ta para kluczy zostanie podpisana przy użyciu klucza prywatnego certyfikatu. Jeśli certyfikat zawiera klucz publiczny RSA, to wygenerowany klucz ECC zostanie podpisany przy użyciu RSA. W przeciwnym razie może zostać podpisany przy użyciu ECDSA. Oczywiście serwer HTTP może obsługiwać oba typy certyfikatów, takie jak certyfikaty ECDSA i RSA.

Przy okazji spójrzmy na jeszcze jeden przykład (zaczerpnięty z innego mojego wpisu TLS: Zestawy szyfrów), który przedstawia opis szyfru wykorzystywanego w komunikacji TLS:

TLS_ECDHE_RSA_WITH_AES_128_CBC_SHA256_P256

Widzimy, że używa on do wymiany kluczy krzywej eliptycznej Diffie-Hellman w wersji efemerycznej (ECDHE), zapewniając poufność przekazywania (Perfect Forward Secrecy). Ponieważ parametry są efemeryczne (tymczasowe), są one odrzucane po użyciu, a wymienionego klucza nie można odzyskać ze strumienia ruchu oraz z pamięci serwera. Następnie, RSA_WITH_AES_128_CBC_SHA256 oznacza, że algorytm uwierzytelniania używany do weryfikacji serwera i podpisywania parametrów wymiany kluczy, klucz prywatny i publiczny oraz sam certyfikat, to RSA. Natomiast wymiana klucza ECDHE jest używana w połączeniu z szyfrem symetrycznym AES-128-CBC, a do uwierzytelnienia wiadomości używany jest skrót SHA256. P256 jest rodzajem krzywej eliptycznej (zestawy szyfrów TLS i krzywe eliptyczne są czasami konfigurowane przy użyciu takiego pojedynczego ciągu).

Jak już wspomniałem wcześniej, zestaw szyfrów jest tak naprawdę zestawem algorytmów potrzebnych do zabezpieczenia połączenia sieciowego za pośrednictwem protokołu SSL/TLS. Klient i serwer kontaktują się ze sobą i wybierają odpowiedni zestaw szyfrów, który będzie używany podczas dalszej komunikacji i wymiany wiadomości. Taki zestaw szyfrów składa się z kilku części (na przykładzie protokołu TLSv1.2):

Co więcej, w przypadku szyfrów wykorzystujących ECDHE oraz ECDH do wymiany kluczy, jesteśmy w stanie sterować krzywymi z poziomu serwera (np. NGINX umożliwia sterowanie nimi z poziomu dyrektywy ssl_ecdh_curve). Natomiast wybór krzywej dla kluczy prywatnych i publicznych oraz certyfikatu odbywa się jedynie na etapie ich tworzenia, np. za pomocą OpenSSL. Aby zobaczyć, że jest to bardzo podobne jak przy wykorzystaniu RSA, utwórzmy najpierw certyfikat TLS wykorzystując krzywą P-256 (secp256k1) a następnie zrobimy to samo z jedną z bezpiecznych krzywych Bernsteina. Możemy wygenerować certyfikat X.509 przy użyciu Ed25519 (lub Ed448) jako naszego algorytmu klucza publicznego, najpierw obliczając klucz prywatny:

# Listujemy wszystkie dostępne krzywe:
openssl ecparam -list_curves

# Generujemy klucze dla P-256: secp256k1:
openssl ecparam -name secp256k1 -genkey -out secp256k1-key.pem
# Weryfikujemy:
openssl pkey -in secp256k1 -key.pem -text

# Generujemy klucze dla X25519 (Ed25519):
openssl genpkey -algorithm ed25519 -out x25519-key.pem
# Weryfikujemy:
openssl pkey -in x25519-key.pem -text

Możesz zauważyć, że pierwsze polecenie nie wyświetli żadnej z krzywych Bernsteina, jest to spowodowane faktem, że implementacja Ed25519 czy Ed448 w OpenSSL działa nieco inaczej niż w przypadku innych krzywych, jednak obie są obsługiwane w OpenSSL 1.1.1 (i nowszych wersjach). Od teraz, mając klucze prywatne i publiczne, można wygenerować CSR, a następnie poprosić o podpisanie go przez urząd certyfikacji. Dla krzywych Bernsteina to oczywiście nie zadziała z publicznie zaufanymi urzędami certyfikacji, takimi jak Digicert lub Let’s Encrypt, ponieważ muszą one ściśle przestrzegać zasad określonych w tzw. podstawowych wymaganiach CA (ang. CA/Browser Forum Baseline Requirements). Na tę chwilę dopuszczają tylko krzywe NIST P-256, P-384 i P-521. Jeśli jednak kontrolujesz urząd certyfikacji w Twojej organizacji, nie powinno być żadnego problemu, aby wykorzystać pozostałe krzywe.

Wiemy już, że aby korzystać z zestawów szyfrów ECDSA, potrzebny jest certyfikat i klucz ECDSA. Aby korzystać z pakietów szyfrów RSA, potrzebujesz certyfikatu i klucza RSA. Certyfikaty ECDSA są zalecane zamiast certyfikatów RSA ze względu na znacznie mniejszy rozmiar klucza oraz ich szybkość jednak to te drugie są częściej wykorzystywane ze względu na ich prostotę, oraz są łatwiejsze do wdrożenia, co jest ich ogromną zaletą. Myślę, że obecnie minimalna konfiguracja zgodna ze standardami branżowymi i zaleceniami profesjonalnych organizacji (Cloudflare, Google czy Mozilla) to ECDSA (256-bit, P-256) lub RSA (2048-bit).

Serwer NGINX obsługuje oba typy certifikatów i dostarcza dyrektywę ssl_certificate_key za pomocą której można ustawić ścieżkę do klucza prywatnego. W Apache natomiast należy wskazać na plik z kluczem prywatnym (również obsługuje oba typy), który odpowiada kluczowi publicznemu w certyfikacie, za pomocą dyrektywy SSLCertificateKeyFile. Plik z kluczem prywatnym powinien być przechowywany w pliku z ograniczonym dostępem, co więcej, musi być możliwy do odczytania przez główny proces usługi jaką wykorzystujesz.

Poniżej znajduje się zrzut ruchu za pomocą narzędzia OpenSSL, który pokazuje różnicę w przypadku obu typów kluczy:

# RSA (4096)
No client certificate CA names sent
Peer signing digest: SHA256
› Peer signature type: RSA-PSS
› Server Temp Key: X25519, 253 bits
[...]
› New, TLSv1.3, Cipher is TLS_AES_256_GCM_SHA384
› Server public key is 4096 bit

# ECC (ECDSA, P-384)
No client certificate CA names sent
Peer signing digest: SHA384
› Peer signature type: ECDSA
› Server Temp Key: X25519, 253 bits
[...]
› New, TLSv1.3, Cipher is TLS_AES_256_GCM_SHA384
› Server public key is 384 bit

Więcej informacji na omówiony w tym rozdziale temat wraz z porównaniem większości krzywych znajdziesz tutaj. Ponadto zapoznaj się z dokumentem Security dangers of the NIST curves [PDF], który opisuje problemy dla krzywych NIST (dyskusje na temat doboru parametrów) oraz porównuje je z krzywą Curve25519. Polecam także przeczytać równie ciekawą prezentacją pod tytułem A riddle wrapped in an Enigma [PDF], w której autorzy poddają ocenie niektóre teorie oraz spekulacje dotyczące NSA, kryptografii krzywych eliptycznych (ECC) oraz kryptografii kwantowo odpornej (ang. quantum-safe cryptography), odnoszącej się do algorytmów kryptograficznych, o których wiadomo, że są odporne na ataki z wykorzystaniem komputerów kwantowych. Jeśli zastanawiasz się, czy istnieją równie wydajnie lub jeszcze wydajniejsze krzywe niż krzywa Curve25519 (oczywiście znalezienie scenariusza, w którym ta dodatkowa prędkość faktycznie robi zauważalną różnicę, jest niezwykle trudna), zapoznaj się z opisem krzywych binarnych opisanych w dokumencie Koblitz curve cryptosystems [PDF].

Jakie są zalecenia co do rozmiaru klucza prywatnego? #

Nie ma jednej odpowiedzi na to pytanie i zależy to tak naprawdę od sytuacji. Aby określić, jaki rozmiar będzie odpowiedni, musisz zadać sobie kilka pytań. Na przykład, ile warte są Twoje dane? Jak długo powinny być bezpieczne? Jakimi zasobami i mocą obliczeniową dysponują atakujący? Nie jest łatwo odpowiedzieć na te pytania.

Certyfikaty SSL najczęściej używają kluczy RSA, zaś zalecany rozmiar tych kluczy rośnie co jakiś czas, aby utrzymać wystarczającą siłę kryptograficzną. Prawda jest taka (zwłaszcza jeśli mówimy o RSA), że przemysł/społeczność są podzielone jeśli chodzi o rozmiar kluczy. Sam jestem w obozie „używaj kluczy RSA 2048-bit, ponieważ 4096-bit nie daje nam obecnie prawie nic, a jednocześnie sporo kosztuje”.

Kluczowe moim zdaniem jest zrozumienie, że mocne strony każdego z rozwiązań stają się tak naprawdę bez znaczenia, gdy zostanie osiągnięta strefa, w której „nie da się złamać kluczy przy użyciu istniejącej technologii, tj. mając odpowiedni sprzęt i czas”. Ponadto zawsze powinniśmy mieć świadomość, że w teorii każdy rozmiar jest dozwolony pod warunkiem spełnienia wymaganej siły bezpieczeństwa. Jednak ocena bezpieczeństwa klucza o danym rozmiarze jest złożoną kwestią. Dobrą praktyką jest myślenie o rozmiarach kluczy jako o pewnym marginesie, czyli gdy bezpieczeństwo osiąga pewien próg, wszystko inne staje się nieistotne i niepotrzebne. Dlatego można zadać pytanie inaczej: jaki rozmiar kluczy należy zapewnić, aby nie istniała obecnie możliwość ich złamania? Myślę, że ciekawą odpowiedź znajdziesz w tym komentarzu.

Inna sprawa jest taka, że nie ma sensownego sposobu, w jaki 3xxx-bitowe i 4xxx-bitowe klucze RSA (Mozilla zaleca takie rozmiary, po więcej informacji zerknij do dokumentu Mozilla Guidelines - Key Management) mogłyby być ze sobą porównywane — z punktu widzenia bezpieczeństwa — i w jakikolwiek sposób uznane za bezpieczniejsze względem np. 2048-bitowych kluczy RSA. Każdy z nich jest tak naprawdę niezniszczalny w dającej się przewidzieć przyszłości. Prawda jest też taka, że klucz RSA o długości 1024 bitów jest obecnie wystarczający do wielu celów o średnim poziomie bezpieczeństwa (moim zdaniem nadaje się bardziej na potrzeby własne). Miejmy jednak świadomość, że taki rozmiar nie jest wystarczający do wszystkiego i raczej należy go unikać, aby zachować poufność danych w przyszłości lub zachować je w tajemnicy przed przeciwnikiem gotowym poświęcić odpowiedni czas i pieniądze.

Myślę, że ciekawe wyjaśnienie dotyczące doboru odpowiedniego rozmiaru znajdziesz w artykule Why some cryptographic keys are much smaller than others.

Co mówią standardy branżowe? #

Jeśli chodzi o zalecany rozmiar kluczy RSA, Eksperci ds. Bezpieczeństwa przewidują, że 2048 bitów będzie wystarczające do użytku komercyjnego do około 2030 roku (zgodnie z normą NIST, patrz także Recommendation for Key Management: Part 1 – General [NIST, PDF]). Moim zdaniem, prognoza bezpieczeństwa dla tego rozmiaru trwająca do 2030 roku może okazać się niewystarczająca ze względu na rosnącą siłę obliczeniową. Amerykańska Agencja Bezpieczeństwa Narodowego (NSA) wymaga, aby wszystkie ściśle tajne pliki i dokumenty były szyfrowane przy użyciu 384-bitowych kluczy ECC (7680-bitowy klucz RSA). OpenSSL wykorzystuje domyślnie klucze o rozmiarze 2048 bit. Ponadto, także ze względów bezpieczeństwa, CA/Browser forum - Baseline Requirements [PDF] i IST zaleca użycie 2048-bitowych certyfikatów/kluczy RSA.

Poniższe porównanie może okazać się bardzo pomocne:

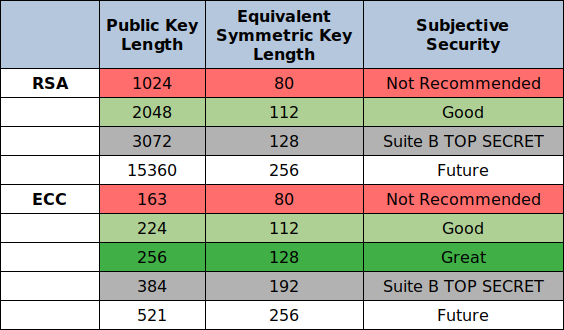
Najnowsza wersja FIPS-186-5 (Draft) [FIPS, PDF] określa zastosowanie modułu, którego długość bitu jest liczbą całkowitą równą 2048-bit lub większą (co ciekawe, starsza wersja, tj. FIPS-186-4 z 2013 roku, mówiła, że rząd federalny USA generuje (i używa) podpisy cyfrowe o długości klucza 1024, 2048 lub 3072 bit).

Co więcej, zalecenia Europejskiej Rady ds. Płatności (EPC342-08 v8.0 [EPC, PDF]) mówią, że należy unikać używania 1024-bitowych kluczy RSA i 160-bitowych kluczy ECC w nowych aplikacjach, z wyjątkiem krótkoterminowej ochrony niekrytycznych aplikacji. EPC zaleca stosowanie co najmniej 2048-bitowego RSA lub 224-bitowego ECC do ochrony średnioterminowej (np. 10-letniej). Klasyfikują także SHA-1, moduły RSA 1024-bit, klucze ECC 160-bit jako odpowiednie do użycia w starszych wersjach (moim zdaniem SHA-1 nie nadaje się do tych zastosowań).

Dokument SSL/TLS Deployment Best Practices (SSL Labs) także opisuje problem rozmiaru klucza w interesujący sposób:

The cryptographic handshake, which is used to establish secure connections, is an operation whose cost is highly influenced by private key size. Using a key that is too short is insecure, but using a key that is too long will result in "too much" security and slow operation. For most web sites, using RSA keys stronger than 2048 bits and ECDSA keys stronger than 256 bits is a waste of CPU power and might impair user experience. Similarly, there is little benefit to increasing the strength of the ephemeral key exchange beyond 2048 bits for DHE and 256 bits for ECDHE.

Wiemy już, że dłuższe klucze RSA zajmują więcej czasu procesora, gdy są używane do szyfrowania i deszyfrowania. Również uzgadnianie sesji SSL/TLS na początku każdego połączenia będzie wolniejsze. Ten typ kryptografii ma również niewielki wpływ na stronę klienta (np. przeglądarki). Podczas korzystania z krzywej Curve25519, ECC jest uważany za bardziej bezpieczny (z założenia jest szybki i odporny na różne ataki). Biorąc pod uwagę stosunkowo duże zasoby obliczeniowe wymagane do obliczania logarytmów dyskretnych, systemy kryptograficzne z krzywą eliptyczną pozwalają znacznie zmniejszyć rozmiar kluczy. Mały rozmiar klucza umożliwia szybsze wykonywanie różnych operacji kryptograficznych. Oczywiście, RSA nie jest mniej bezpieczny, co więcej, pod względem praktycznym jest również uważany za „niezniszczalny”.

Chociaż prawdą jest, że dłuższy klucz zapewnia lepsze bezpieczeństwo, podwajając długość klucza RSA z 2048 do 4096, wzrost bitów bezpieczeństwa wynosi tylko 18, czyli zaledwie 16%. Co więcej, czas na podpisanie wiadomości wzrasta nawet 7 razy, a w niektórych przypadkach czas weryfikacji podpisu zwiększa się ponad 3-krotnie! Ponadto, poza wymaganiem większej przestrzeni dyskowej (jest to co prawda minimalny skutek uboczny ich stosowania), dłuższe klucze przekładają się również na zwiększone wykorzystanie procesora.

Niewątpliwie największe postępy zostały poczynione w przypadku problemu faktoryzacji i łamania algorytmu RSA. Obecnie jedynym zagrożeniem dla tego algorytmu (a także dla ECC) są komputery kwantowe i ew. implementacja algorytmu faktoryzacji Petera Shora [PDF]. Natomiast największym kluczem RSA, jaki udało sie rozłożyć na czynniki pierwsze, jest klucz 768-bitowy (źródło: Factorization of a 768-bit RSA modulus [PDF]). Dokonano tego 12 grudnia 2009 r. Co więcej, nie są znane przypadki odszyfrowania informacji zakodowanych współczesnymi, 1024-bitowymi i dłuższymi kluczami asymetrycznymi, bez znajomości odpowiednich kluczy prywatnych, jednak był to sygnał dla wielu dostawców, którzy zaczęli masowo przechodzić na klucze o większym rozmiarze.

Spójrz na porównanie rozmiaru kluczy przedstawiające dodatkowo kilka istotnych informacji:

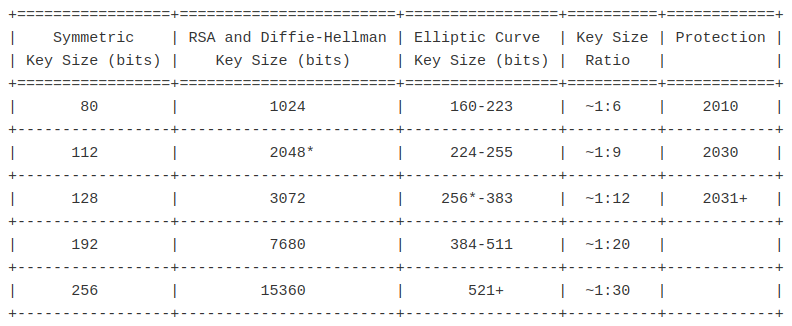
* zalecane rozmiary kluczy RSA i ECC

Powyższa tabela mówi o jednej bardzo istotnej rzeczy. Otóż rozmiar klucza publicznego jest istotny, jednak równie istotny jest dobór odpowiedniego klucza wykorzystującego kryptografię symetryczną (jeżeli wykorzystujemy system mieszany). Długości kluczy dla każdego rodzaju kryptografii powinny być tak dobrane, aby równie trudne było zaatakowanie systemu za pomocą każdego możliwego mechanizmu. Nie ma sensu używać algorytmu symetrycznego z kluczem 128-bitowym razem z algorytmem klucza publicznego z kluczem 512-bitowym lub 160-bit dla ECC. Tak samo jak nie ma sensu używać algorytmu symetrycznego z kluczem 64-bitowym razem z kluczem publicznym o rozmiarze 2048-bit.

Pamiętajmy, że każdy system zostanie najprawdopodobniej zaatakowany w jego najsłabszym punkcie, dlatego, aby zachować odpowiedni poziom bezpieczeństwa, w przypadku wyboru algorytmu symetrycznego o rozmiarze np. 112-bit, powinieneś wybrać długość modułu dla swojego algorytmu klucza publicznego około 2048-bit. Eksperci zalecają jednak stosowanie kluczy publicznych o bezpieczniejszym rozmiarze niż długość klucza symetrycznego. Klucze publiczne generalnie pozostają dłużej w bezpiecznej granicy i służą do ochrony większej ilości informacji.

Zasadniczo nie ma istotnego powodu, aby wybierać klucze RSA 3xxx lub 4xxx-bitowe. Tak naprawdę prawdziwą zaletą ich stosowania jest zabezpieczenie na przyszłość. Jeśli jednak chcesz uzyskać ocenę (bo klient ma takie wymagania lub jeśli chcesz się pochwalić przed innymi) A+ oraz 100% dla Key Exchange skanera SSL Labs, zdecydowanie powinieneś użyć 4096-bitowych kluczy prywatnych. Według mnie są to obecnie jedyne powody, dla których powinieneś ich używać. Twojej ocenie pozostawiam czy aż tak istotne.

Jako podstawowe źródło określające zalecane rozmiary kluczy w odniesieniu do czasu ich przydatności traktuj serwis keylength, który odwołuje się do dokumentów, na których opierają się zalecenia branżowe. Znajduje się tam podsumowanie z raportów znanych organizacji, dzięki czemu można porównać wszystkie obecnie dostępne techniki szyfrowania i znaleźć odpowiednią długość klucza dla pożądanego poziomu ochrony.

Podsumowując to wszystko, myślę, że rekomendacją oraz odpowiedzią na pytanie zadane w tytule jest: używaj kluczy prywatnych RSA min. 2048-bit lub ECC min. 256-bit, które zapewniają obecnie odpowiedni poziom bezpieczeństwa.

Dlaczego długość klucza jest ważna ale nie kluczowa? #

W przypadku użycia kluczy RSA 2048-bit oraz ECC z zakresu od 224-bit do 256-bit (czyli granicy, powyżej której wszystko jest uznawane za bezpieczne) istnieje, moim zdaniem, jeden ważny warunek, na który powinieneś zwrócić uwagę. Stosowanie kluczy o takich rozmiarach powinno iść w parze z rozsądnymi interwałami ważności (np. nie więcej niż 6-12 miesięcy dla 2048-bitowego klucza i certyfikatu; organizacja Let’s Encrypt daje 90 dni życia certyfikatom), aby dać atakującemu mniej czasu na złamanie klucza i zminimalizować prawdopodobieństwo, że ktoś wykorzysta wszelkie luki, które mogą wystąpić w przypadku naruszenia jego bezpieczeństwa. Ponadto, zgodnie z pracami oragnizacji CA/Browser (CA/B) Forum polegającymi na skróceniu żywotności certyfikatów, wiele urzędów certyfikatcji i firm przechodzi na certyfikaty o krótszej ważności (patrz: SSL Certificate Validity Will Be Limited to One Year by Apple’s Safari Browser). Możesz o tym pomyśleć jak o hasłach, które regularnie zmieniasz i z tego samego powodu powinieneś zachować regularność zmiany kluczy.

Ponadto uważam, że powinniśmy bardziej martwić się o to, że nasze klucze prywatne zostaną skradzione w wyniku naruszenia bezpieczeństwa serwera, a nie złej konfiguracji parametrów SSL/TLS. Zapewnienie odpowiedniego bezpieczeństwa kluczy prywatnych (ustawione hasło, uprawnienia, cykliczna rotacja czy tajność) powinno być jednym z najważniejszych czynników, ponieważ przy niespełnieniu tych warunków, poziom bezpieczeństwa całego systemu może zostać znacznie obniżony, a nawet kompletnie wyeliminowany. Pamiętaj, że ciągły postęp technologiczny naraża nasz klucz na ataki przez co, to ochrona klucza prywatnego jest kluczowa, ponieważ jeśli wpadnie on w niepowołane ręce, wszystkie rozważania dotyczące jego rozmiaru oraz pozostałych parametrów protokołu SSL/TLS nie będą miały żadnego znaczenia. Oczywiście nie oznacza to, że rozmiar kluczy i parametry są nieistotne — są bardzo istotne. Jednak zbyt często skupiamy się na rozmiarze kluczy, który oczywiście jest bardzo ważny, a nie na pozostałych niezwykle istotnych parametrach. Dzieje się tak głównie dlatego, że rozmiar klucza jest jedyną rzeczą, którą w pewnym sensie rozumiemy.

Uważam, że podczas doboru rozmiaru kluczy powinniśmy przyjąć rozsądne i dosyć konserwatywne podejście. Aby określić, jaki rozmiar jest odpowiedni oraz potrzebny, musisz przyjrzeć się zabezpieczeniu i żywotności, jakie prezentuje każde z rozwiązań, oraz aktualnemu stanowi możliwości faktoringu. Jako administrator powinieneś także być na bieżąco ze standardami branżowymi oraz zaleceniami szanowanych organizacji, ponieważ niezwykle ważne jest, aby regularnie sprawdzać używane produkty ze względu na charakter rozwoju technologicznego. Zaleca się, aby każde rozwiązanie, które wdrażasz, spełniały aktualne standardy, takie jak FIPS 140-2 [NIST, PDF] czy NIST 800-131A Revision 2 [NIST, PDF]. Niezależnie od tego, jakie zdanie masz na temat standardów, brak formalnej pewności we wdrożeniach TLS oznacza, że ​​mogą występować pewne niedociągnięcia. Korzystanie z najnowszych zaleceni oraz obsługiwanych i w pełni poprawionych wersji implementacji TLS pomoże w zarządzaniu tym ryzykiem.

Przytoczę jeszcze cytat z książki Applied Cryptography: Protocols, Algorithms, and Source Code in C, której autorem jest Bruce Schneier, światowej klasy kryptolog:

The security of a cryptosystem should rest in the key, not in the details of the algorithm.

Fakt jest taki, że klucze o rozmiarze 1024-bit zapewniają obecnie minimalny poziom bezpieczeństwa. Jednak wiemy, że granica bezpieczeństwa, którą określają klucze o takim rozmiarze, jest już bliska. Jeśli chcesz, aby Twoje klucze pozostały bezpieczne przez kilka następnych lat, 1024 bity jest prawdopodobnie (a nawet zdecydowanie) za krótkie. Warto wybrać klucze, które będą odporne na ewentualne niespodzianki w przyszłości, a obecnie zalecane minimum to 2048-bit do roku 2030 i 3072-bit po 2030 r.

Podsumowanie #

Myślę, że jeśli kiedykolwiek znajdziemy się w świecie, w którym 2048-bitowe klucze RSA nie będą już wystarczająco dobre, nie będzie to wcale spowodowane możliwością ich zastąpienia większymi kluczami, tylko dlatego, że RSA stanie się po prostu przestarzałe jako technologia w opozycji do rewolucyjnych osiągnięć komputerowych. Dlatego, moim zdaniem, większa długość klucza staje się całkowicie nieistotna w obecnych czasach.

Głównymi problemami algorytmu RSA i długości kluczy są zapotrzebowanie na zasoby i moc obliczeniową, która wymagana jest do wykonania operacji na kluczach prywatnych i publicznych, oraz, podczas ich generowania. Co więcej, moim zdaniem najsłabszym ogniwem w szyfrowaniu RSA są wady implementacyjne, a nie zdolność do liczenia dużych liczb pierwszych (która jest oczywiście procesem czasochłonnym) czy możliwość złamania wystarczająco długich kluczy. Jeśli tak się stanie, 3072 lub 4096 bitów i tak nie zrobi dużej różnicy. Właśnie dlatego wszystko powyżej 2048 bitów jest ogólnie uważane za rodzaj bardzo mocnego przerysowania, jeśli chodzi o bezpieczeństwo w dzisiejszych czasach. Historia kryptografii pokazuje, że dobre algorytmy kryptograficzne zostały złamane nie z powodu złej matematyki, ale z powodu złej implementacji dobrej matematyki. Żaden z omawianych algorytmów szyfrowania nie zapewni optymalnego bezpieczeństwa, jeśli jest nieprawidłowo zaimplementowany i nie spełnia standardów branżowych.

Najlepszym obecnie rozwiązaniem problemów szyfrowania RSA jest zastosowanie kryptografii opartej na krzywych eliptycznych, głównie ze względu na opłacalność ich stosowania w kontekście podpisywania i deszyfrowania (zwłaszcza w małych układach mikroprocesorowych) — obecnie możemy być pewni matematycznego bezpieczeństwa ECDSA (poza kilkoma pytaniami dotyczącymi wyboru krzywej oraz zapewnieniu odpowiednio losowych lub nieprzewidywalnych danych jako danych wejściowych). Najnowocześniejsze i zalecane przez wszystkich systemy ECC to X25519 dla wymiany kluczy i Ed25519 dla podpisów cyfrowych. Zasadniczo wszyscy zgadzają się, że są one lepsze niż NIST P-256 dla ECDH i ECDSA. Wadą niestety jest słabsze wsparcie. Pamiętaj jednak, że w przypadku certyfikatów serwera TLS 2048-bitowe klucze RSA zapewniają obecnie chyba najlepsze połączenie bezpieczeństwa, wydajności i wsparca po stronie serwera i klienta.

Dodatkowe zasoby #

Podobne posty